Question

An inductance $L$ and a resistance $R$ are connected to a battery. After some time, the battery is removed but $L$ and $R$ remain connected in the closed circuit. The value of current will reduce to \[37\% \] of its maximum value in
A. $RL{\text{ second}}$
B. $\dfrac{R}{L}{\text{ second}}$
C. $\dfrac{L}{R}{\text{ second}}$
D. $\dfrac{1}{{LR}}{\text{ second}}$

Answer 1

Hint:To solve this type of question we will use the concept of decay of current.If a circuit containing a pure inductor L and a resistor R in series with a battery and a key is opened then the current starts to flow from the charge capacitor. After this there will be mathematical terms and we will get our required answer.

Formula used:
\[i = {i_0}({e^{ - \dfrac{{RT}}{L}}})\]
Where, $i$ is the current, ${i_0}$ is the initial current, $R$ is the resistance, $T$ is the time and $L$ is the inductance.

Complete step by step answer:
According to the question we can understand that after removal of the battery there is a reduction in current value of $37\% $.

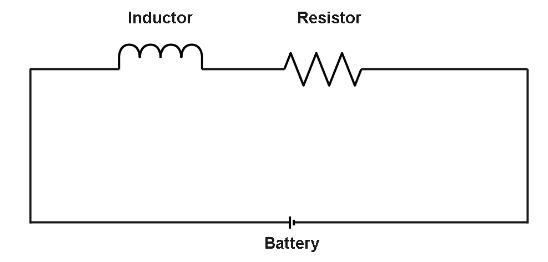
So, we can say that rate of decay of current is,
\[i = {i_0}({e^{ - \dfrac{{RT}}{L}}})\]
Now, putting the values in above equation,
\[0.37{i_0} = {i_0}({e^{ - \dfrac{{RT}}{L}}}) \\
\Rightarrow 0.37 = {e^{ - \dfrac{{RT}}{L}}} \\ \]
And we know that $0.37$ is approximately equivalent to $\dfrac{1}{e}$. Therefore,
$\dfrac{1}{e} = {e^{ - \dfrac{{RT}}{L}}}$
We know that,
$\log {e^{ - 1}} = \log {e^{\dfrac{{ - RT}}{L}}}$
Therefore,
$- 1 = \dfrac{{ - RT}}{L} \\
\therefore T = \dfrac{L}{R} \\ $
Hence the correct option is C.

Note:We must know that the time constant in the LR circuit is used to describe the speed of the current attaining its maximum steady value. Hence the time constant is used to measure the speed of the LR circuit.