Question

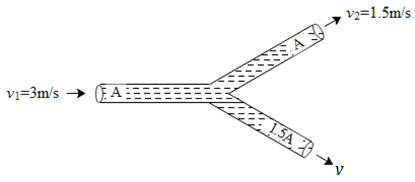
An incompressible liquid flows through a horizontal tube as shown in the following figure. Then velocity v of the fluid is

Answer 1

Hint: Assume that the liquid is non viscous and flows steadily. In the above diagram we can see that the liquid flows from one tube and splits into two. Since the mass of the liquid flowing from the initial tube to the other two tubes in unit time remains the same, we can use the equation of continuity to determine the velocity of the liquid across the cross sectional area i.e. 1.5A.

Formula used:
$A{{v}_{1}}=A{{v}_{2}}+(1.5)Av$

Complete step-by-step answer:
If we see the above diagram, we can see that the liquid flows from one tube and then divides into two different tubes. Whatever mass flows across the single tube in unit time the same will get divided into the two other tubes. Hence we will use the equation of continuity to determine the velocity ‘v’ across the cross section 1.5A. Let us say that a liquid flows from a cross section ‘A’ with velocity ‘v’ to another cross section ‘a’ with velocity V. Hence the equation of continuity is given by,
$Av=aV$
If the same liquid splits into n tubes having the different cross sectional areas than the above equation becomes,
$\begin{align}
  & Av={{a}_{1}}{{V}_{1}}+{{a}_{2}}{{V}_{2}}....{{a}_{n}}{{V}_{n}} \\
 & \Rightarrow Av=\sum\limits_{i=1}^{n}{{{a}_{i}}{{V}_{i}}} \\
\end{align}$
Applying the above equation to the Y shaped tube in the above diagram we get,
$\begin{align}
  & A{{v}_{1}}=A{{v}_{2}}+1.5Av \\
 & \Rightarrow A{{v}_{1}}=A({{v}_{2}}+1.5v) \\
 & \Rightarrow 3m{{s}^{-1}}=1.5m{{s}^{-1}}+1.5v \\
 & \Rightarrow 1.5=1.5v \\
 & \Rightarrow v=1m{{s}^{-1}} \\
\end{align}$
Hence the velocity of the liquid flowing across the tube of cross sectional area 1.5A is equal to 1m/s.

Note: The equation of continuity is the special case of law of conservation of mass. The equation shows that velocity of the liquid is inversely proportional to the cross sectional area of the tube or the pipe. If the liquid is viscous and does not flow steadily than the above equation is no longer valid.