
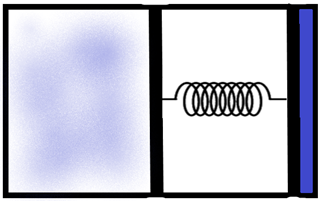
An ideal monoatomic gas is confined in a horizontal cylinder by a spring-loaded piston. Initially, the gas is at temperature \[{{T}_{1}}\], pressure \[{{P}_{1}}\] and volume \[{{V}_{1}}\] and the spring is in its relaxed state. The gas is then heated very slowly to temperature \[{{T}_{2}}\], pressure \[{{P}_{2}}\] and volume \[{{V}_{2}}\]. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement/s is/are –
A) If \[{{V}_{2}}=2{{V}_{1}}\text{ and }{{\text{T}}_{2}}=3{{T}_{1}}\], then the energy store in the spring is \[\dfrac{1}{4}{{P}_{1}}{{V}_{1}}\]
B) If \[{{V}_{2}}=2{{V}_{1}}\text{ and }{{\text{T}}_{2}}=3{{T}_{1}}\], then the change in internal energy is \[3{{P}_{1}}{{V}_{1}}\]
C) If \[{{V}_{2}}=3{{V}_{1}}\text{ and }{{\text{T}}_{2}}=4{{T}_{1}}\], then the work done by the gas is \[\dfrac{7}{3}{{P}_{1}}{{V}_{1}}\]
D) If \[{{V}_{2}}=3{{V}_{1}}\text{ and }{{\text{T}}_{2}}=4{{T}_{1}}\], then the heat supplied to the gas is \[\dfrac{17}{6}{{P}_{1}}{{V}_{1}}\].

Answer
567.3k+ views
Hint: We need to understand the mechanisms involved and the relation between the thermodynamic variables – the pressure, volume and temperature – with the energy in the system or work done by the system as required in the problem.
Complete step by step solution:
We are given a piston which is built with a spring loaded to it as shown in the figure. We know that for a system of ideals, when the temperature increases, the pressure inside it increases, which in this case causes the piston to be pressed causing a subsequent increase in the volume also.
Now, let us consider the piston. The total area of the piston base where the gas molecules exert the pressure is ‘A’. We can calculate the total pressure acting on the piston as the initial pressure in the system and the force due to the spring of spring constant ‘k’ as –
\[\begin{align}
& {{P}_{2}}={{P}_{1}}+{{P}_{spring}} \\
& \therefore {{P}_{2}}={{P}_{1}}+\dfrac{kx}{A} \\
\end{align}\]
Now, we know from the gas law that –
\[\begin{align}
& \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}} \\
& \Rightarrow \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}2{{V}_{1}}}{3{{T}_{1}}} \\
& \therefore {{P}_{2}}=\dfrac{3}{2}{{P}_{1}} \\
\end{align}\]
Also, the ‘x’ is the ratio of the volume and the area. So, we can find the ‘kx’ as –
\[\begin{align}
& {{P}_{2}}=\dfrac{3}{2}{{P}_{1}} \\
& \Rightarrow \dfrac{3}{2}{{P}_{1}}={{P}_{1}}+\dfrac{kx}{A} \\
& \therefore kx=\dfrac{{{P}_{1}}A}{2} \\
\end{align}\]
This can be used to find the energy stored in the spring as –
\[\begin{align}
& {{E}_{spring}}=\dfrac{1}{2}k{{x}^{2}} \\
& \Rightarrow {{E}_{spring}}=\dfrac{1}{2}\dfrac{{{P}_{1}}A}{2}\dfrac{{{V}_{1}}}{A} \\
& \therefore {{E}_{spring}}=\dfrac{1}{4}{{P}_{1}}{{V}_{1}} \\
\end{align}\]
We can find the change in internal energy of the monoatomic ideal gas as –
\[\begin{align}
& \Delta U=\dfrac{3}{2}({{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}) \\
& \Rightarrow \Delta U=\dfrac{3}{2}(\dfrac{3}{2}{{P}_{1}}2{{V}_{1}}-{{P}_{1}}{{V}_{1}}) \\
& \therefore \Delta U=3{{P}_{1}}{{V}_{1}} \\
\end{align}\]
Now, let us consider the situation when –
\[{{V}_{2}}=2{{V}_{1}}\text{ and }{{\text{T}}_{2}}=4{{T}_{1}}\]
Applying the gas law, we get the final pressure as –
\[\begin{align}
& \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}} \\
& \Rightarrow \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}3{{V}_{1}}}{4{{T}_{1}}} \\
& \therefore {{P}_{2}}=\dfrac{4}{3}{{P}_{1}} \\
\end{align}\]
Also, the distance ‘x’ becomes –
\[x=\dfrac{2{{V}_{1}}}{A}\]
The work done by the gas in this situation can be given as –
\[\begin{align}
& {{W}_{gas}}=-({{W}_{atm}}+{{W}_{spring}}) \\
& \Rightarrow {{W}_{gas}}=-({{P}_{1}}{{V}_{1}}+\dfrac{1}{2}k{{x}^{2}}) \\
& \Rightarrow {{W}_{gas}}=-({{P}_{1}}A\dfrac{2{{V}_{1}}}{A}+\dfrac{1}{2}\dfrac{{{P}_{1}}A2{{V}_{1}}}{3A}) \\
& \Rightarrow {{W}_{gas}}=-(2{{P}_{1}}{{V}_{1}}+\dfrac{{{P}_{1}}{{V}_{1}}}{3})=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3} \\
\end{align}\]
Now, the total energy of the system due to heating can be given as –
\[\begin{align}
& \Delta Q=W+\Delta U \\
& \Rightarrow \Delta Q=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3}+\dfrac{3}{2}({{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}) \\
& \Rightarrow \Delta Q=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3}+\dfrac{3}{2}(\dfrac{4}{3}{{P}_{1}}3{{V}_{1}}-{{P}_{1}}{{V}_{1}}) \\
& \therefore \Delta Q=-\dfrac{41}{6}{{P}_{1}}{{V}_{1}} \\
\end{align}\]
We can see that these are the required solutions.
The correct answers are options A, B and C.
Note:
Any system which is free to expand will keep on expanding with an increase in the temperature of the system by the virtue of heat energy. The total energy in the system is given to the increase in internal energy and for the work done on the container.
Complete step by step solution:
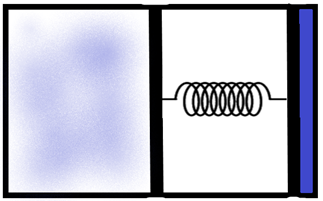
We are given a piston which is built with a spring loaded to it as shown in the figure. We know that for a system of ideals, when the temperature increases, the pressure inside it increases, which in this case causes the piston to be pressed causing a subsequent increase in the volume also.
Now, let us consider the piston. The total area of the piston base where the gas molecules exert the pressure is ‘A’. We can calculate the total pressure acting on the piston as the initial pressure in the system and the force due to the spring of spring constant ‘k’ as –
\[\begin{align}
& {{P}_{2}}={{P}_{1}}+{{P}_{spring}} \\
& \therefore {{P}_{2}}={{P}_{1}}+\dfrac{kx}{A} \\
\end{align}\]

Now, we know from the gas law that –
\[\begin{align}
& \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}} \\
& \Rightarrow \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}2{{V}_{1}}}{3{{T}_{1}}} \\
& \therefore {{P}_{2}}=\dfrac{3}{2}{{P}_{1}} \\
\end{align}\]
Also, the ‘x’ is the ratio of the volume and the area. So, we can find the ‘kx’ as –
\[\begin{align}
& {{P}_{2}}=\dfrac{3}{2}{{P}_{1}} \\
& \Rightarrow \dfrac{3}{2}{{P}_{1}}={{P}_{1}}+\dfrac{kx}{A} \\
& \therefore kx=\dfrac{{{P}_{1}}A}{2} \\
\end{align}\]
This can be used to find the energy stored in the spring as –
\[\begin{align}
& {{E}_{spring}}=\dfrac{1}{2}k{{x}^{2}} \\
& \Rightarrow {{E}_{spring}}=\dfrac{1}{2}\dfrac{{{P}_{1}}A}{2}\dfrac{{{V}_{1}}}{A} \\
& \therefore {{E}_{spring}}=\dfrac{1}{4}{{P}_{1}}{{V}_{1}} \\
\end{align}\]
We can find the change in internal energy of the monoatomic ideal gas as –
\[\begin{align}
& \Delta U=\dfrac{3}{2}({{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}) \\
& \Rightarrow \Delta U=\dfrac{3}{2}(\dfrac{3}{2}{{P}_{1}}2{{V}_{1}}-{{P}_{1}}{{V}_{1}}) \\
& \therefore \Delta U=3{{P}_{1}}{{V}_{1}} \\
\end{align}\]
Now, let us consider the situation when –
\[{{V}_{2}}=2{{V}_{1}}\text{ and }{{\text{T}}_{2}}=4{{T}_{1}}\]
Applying the gas law, we get the final pressure as –
\[\begin{align}
& \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}} \\
& \Rightarrow \dfrac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\dfrac{{{P}_{2}}3{{V}_{1}}}{4{{T}_{1}}} \\
& \therefore {{P}_{2}}=\dfrac{4}{3}{{P}_{1}} \\
\end{align}\]
Also, the distance ‘x’ becomes –
\[x=\dfrac{2{{V}_{1}}}{A}\]
The work done by the gas in this situation can be given as –
\[\begin{align}
& {{W}_{gas}}=-({{W}_{atm}}+{{W}_{spring}}) \\
& \Rightarrow {{W}_{gas}}=-({{P}_{1}}{{V}_{1}}+\dfrac{1}{2}k{{x}^{2}}) \\
& \Rightarrow {{W}_{gas}}=-({{P}_{1}}A\dfrac{2{{V}_{1}}}{A}+\dfrac{1}{2}\dfrac{{{P}_{1}}A2{{V}_{1}}}{3A}) \\
& \Rightarrow {{W}_{gas}}=-(2{{P}_{1}}{{V}_{1}}+\dfrac{{{P}_{1}}{{V}_{1}}}{3})=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3} \\
\end{align}\]
Now, the total energy of the system due to heating can be given as –
\[\begin{align}
& \Delta Q=W+\Delta U \\
& \Rightarrow \Delta Q=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3}+\dfrac{3}{2}({{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}) \\
& \Rightarrow \Delta Q=-\dfrac{7{{P}_{1}}{{V}_{1}}}{3}+\dfrac{3}{2}(\dfrac{4}{3}{{P}_{1}}3{{V}_{1}}-{{P}_{1}}{{V}_{1}}) \\
& \therefore \Delta Q=-\dfrac{41}{6}{{P}_{1}}{{V}_{1}} \\
\end{align}\]
We can see that these are the required solutions.
The correct answers are options A, B and C.
Note:
Any system which is free to expand will keep on expanding with an increase in the temperature of the system by the virtue of heat energy. The total energy in the system is given to the increase in internal energy and for the work done on the container.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




