Question

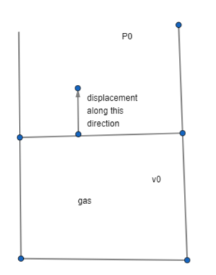
An ideal gas is contained in a piston cylinder arrangement as shown in figure. The area of the piston is A and its mass is m. The surrounding Atmospheric pressure is ${{P}_{0}}$. Under equilibrium condition, the volume of the gas is ${{V}_{0}}$. Find the angular frequency of small vertical oscillation of the piston assuming the expansion and compression of the gas to be adiabatic (adiabatic constant = $\gamma $)

Answer 1

Hint: Consider the motion of the piston. Starting from the adiabatic gas law Find out the force on the piston. Then comparing it with simple harmonic motion, find the value of k. Then we can find the angular frequency of oscillation.

Formula used:
$P{{V}^{\gamma }}=\text{constant}$
$F=A\Delta P$
$\omega =\sqrt{\dfrac{k}{M}}$

Complete step by step answer:
The surrounding atmospheric pressure is ${{P}_{0}}$and the volume of the gas at equilibrium is ${{V}_{0}}$.
Let the piston have moved or displaced by a distance x above the equilibrium position.
So, increased in volume will be $\Delta v=Ax$
Where A is the area of the piston.
The process is adiabatic. So, we can write,
$P{{V}^{\gamma }}=\text{constant}$
Where P is the pressure, v is the volume and $\gamma $ is the adiabatic constant.
Taking log on the above equation we get,
$\begin{align}
  & \ln \left( P{{V}^{\gamma }} \right)=\ln \left( \text{constant} \right) \\
 & \ln P+\ln {{V}^{\gamma }}=0 \\
 & \ln P+\gamma \ln V=0 \\
\end{align}$
Now, differentiating the above equation in both sides,
$\begin{align}
  & \dfrac{\Delta P}{p}+\gamma \dfrac{\Delta V}{V}=0 \\
 & \Delta P=-\gamma P\dfrac{\Delta V}{V} \\
\end{align}$
Since, the displacement of the piston is very small we can write,
$\Delta P=-\gamma {{P}_{0}}\dfrac{\Delta V}{{{V}_{0}}}$
where${{P}_{0}}\And {{V}_{0}}$are atmospheric pressure outside the cylinder and the volume of the gas at equilibrium respectively.
Now, the resultant force will be,
$F=A\Delta P$
Putting the value of $\Delta P$ in the above equation we get,
$F=-A\gamma {{P}_{0}}\dfrac{\Delta V}{{{V}_{0}}}$
Putting the value of $\Delta V=Ax$,
$F=-{{A}^{2}}\dfrac{\gamma {{P}_{0}}}{{{V}_{0}}}x$
Compared with the $F=-kx$, we can say that our system is executing simple harmonic motion.
So, we can write,
$k={{A}^{2}}\gamma \dfrac{{{P}_{0}}}{{{V}_{0}}}$
Now, we can find the angular frequency from the value of k by using the following equation.
$\omega =\sqrt{\dfrac{k}{M}}$
Where $\omega $ is the angular frequency and M is the mass of the moving piston.
$\begin{align}
  & \omega =\sqrt{\dfrac{k}{M}} \\
 & \omega =\sqrt{\dfrac{{{A}^{2}}\gamma {{P}_{0}}}{{{V}_{{{0}_{{}}}}}M}} \\
\end{align}$
So, the value of the angular frequency will be $\omega =\sqrt{\dfrac{{{A}^{2}}\gamma {{P}_{0}}}{{{V}_{{{0}_{{}}}}}M}}$

Note: If in a thermodynamic process there is no exchange of heat between the system and surrounding during the process, the process is called adiabatic. It can be either reversible or irreversible.
The adiabatic constant can be defined as the ratio of heat capacity at constant pressure to the heat capacity at constant volume.