Question

An ice cream cone is the union of a right circular cone and a hemisphere that has the same circular base as the cone. Find the volume of the ice cream, if the height of the cone 9 cm and the radius of its base is 2.5 cm.

Answer 1

Hint: In the given question, it is clearly said that the ice cream has two parts. One is the hemispherical part and the other one is the right circular cone part. So, firstly we will find the volume of the hemisphere $\dfrac{2}{3}\pi {{r}^{3}}$ and then we find volume of right circular cone $\dfrac{1}{3}\pi {{r}^{2}}h$ . Finally after adding these two volumes we will get the resultant volume of that ice cream.

Complete step-by-step answer:

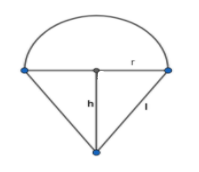
Let us consider an ice cream having its height ‘h’, radius of its base as ‘r’ and ‘l’ as its slant height.
It is given that the height of the ice cream (h)= 9 cm
And the radius of its base (r) = 2.5 cm
Now we will find the volume of hemisphere (${{v}_{1}}$ )
$=\dfrac{2}{3}\pi {{r}^{3}}\cdots (i)$
Also the volume of the right circular cone $({{v}_{2}})$
$=\dfrac{1}{3}\pi {{r}^{2}}h\cdots (ii)$
Therefore the volume of the resulting ice cream (V) i.e. on adding the equations (i) & (ii),
$\begin{align}
  & ={{v}_{1}}+{{v}_{2}} \\
 & =\dfrac{2}{3}\pi {{r}^{3}}+\dfrac{1}{3}\pi {{r}^{2}}h \\
 & =\dfrac{\pi {{r}^{2}}}{3}(2r+h) \\
\end{align}$
Now, we will be substituting the value for r = 2.5 cm and h = 9 cm
$\begin{align}
  & =\dfrac{22\times 2.5\times 2.5}{3\times 7}(2\times 2.5+9) \\
 & =\dfrac{22\times 2.5\times 2.5\times 14}{3\times 7} \\
 & =91.67c{{m}^{3}} \\
\end{align}$
Hence the volume of the ice cream is $91.67c{{m}^{3}}$ .
Note: For the ice cream, the radius of base for the hemisphere and the cone part is the same. Before solving any question regarding mensuration , a good command about figures as well as formulas for each figure must be required. In some questions, they might not give all the values directly for e.g.; the question will give you the value of slant height (l) and then find the volume. Formula for slant height is given below
$\begin{align}
  & \Rightarrow {{l}^{2}}={{r}^{2}}+{{h}^{2}} \\
 & \Rightarrow l=\sqrt{({{r}^{2}}+{{h}^{2}})} \\
\end{align}$