Question

An equilateral triangle is inscribed in the parabola ${{y}^{2}}=4ax$, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
A. $8\sqrt{3}a$
B. $4\sqrt{3}a$
C. $2\sqrt{3}a$
D. $\sqrt{3}a$

Answer 1

Hint: We first try to draw the parabola and the inscribed triangle. We assume the x value for the other two vertices and then find the coordinates of those vertices. We use the equal side length for the triangle to find the relation between $h$ and $a$.

Complete step by step answer:
Let us draw the parabola ${{y}^{2}}=4ax$ and the inscribed triangle where one vertex is at the vertex of the parabola. The general equation of parabola is ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$. For the general equation $\left( \alpha ,\beta \right)$ is the vertex. 4a is the length of the latus rectum. The coordinate of the focus is $\left( \alpha ,\beta +a \right)$. This gives the vertex as $\left( 0,0 \right)$. The length of the latus rectum is $4a$. Therefore, one vertex of the triangle is $A\left( 0,0 \right)$.

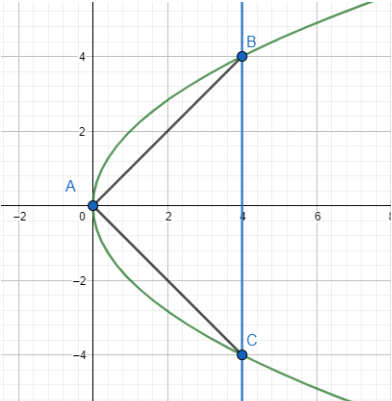
Let us take the other two vertices for $x=h$. The vertices are on the parabola. So, putting the value of $x=h$ on ${{y}^{2}}=4ax$, we get ${{y}^{2}}=4ah$ which gives $y=\pm 2\sqrt{ah}$.Therefore, the other two vertices are $B\left( h,2\sqrt{ah} \right)$ and $C\left( h,-2\sqrt{ah} \right)$. Now this is an equilateral triangle which means all the sides are equal. So, $AB=BC$.We know that the distance between two points $\left( m,n \right)$ and $\left( o,p \right)$ is $\sqrt{{{\left( m-o \right)}^{2}}+{{\left( n-p \right)}^{2}}}$.

We find the length of the sides and get
$AB=\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( 2\sqrt{ah}-0 \right)}^{2}}}=\sqrt{{{h}^{2}}+4ah}$
$\Rightarrow BC=\sqrt{{{\left( h-h \right)}^{2}}+{{\left( 2\sqrt{ah}+2\sqrt{ah} \right)}^{2}}}=\sqrt{16ah}$
The equation $AB=BC$ gives \[\sqrt{{{h}^{2}}+4ah}=\sqrt{16ah}\]. Simplifying we get
\[\sqrt{{{h}^{2}}+4ah}=\sqrt{16ah} \\
\Rightarrow {{h}^{2}}+4ah=16ah \\ \]
Now we try to find the value of $h$ with respect to the value of $a$.
As $h\ne 0$ we get
\[{{h}^{2}}+4ah=16ah \\
\Rightarrow {{h}^{2}}=12ah \\
\Rightarrow h=12a \\ \]
Putting the value of \[h=12a\] in $BC=\sqrt{16ah}$. We get
$BC=\sqrt{16ah} \\
\Rightarrow BC=\sqrt{16a\times 12a}$
$\Rightarrow BC=\sqrt{16a\times 12a} \\
\therefore BC=8\sqrt{3}a$

Hence, the correct option is A.

Note: We also can use the slope of the line AB. The angle for the equilateral triangle will be ${{60}^{\circ }}$. Therefore, the value of the slope $\dfrac{2\sqrt{ah}-0}{h-0}=\tan 60$. We simplify the equation and find the relation between $h$ and $a$ to use for the sides’ length.