Question

An energy sources will supply a maximum current into the load if its internal resistance is
A. Zero
B. non zero but less than the resistance of the load
C. equal to the resistance of the load
D. very large as compared to the load resistance

Answer 1

Hint: Consider a simple closed circuit with a battery of some emf and internal resistance and a load resistance. Using the formula for the effective resistance of two resistances connected in series , Ohm’s law finds an expression for the current in the circuit. Then you can analyse the equation and find the value of internal resistance for which current is maximum.

Formula used:
${{R}_{eq}}=R+r$
$E=i{{R}_{eq}}$
$E$ is the emf of the cell, $R$ is load resistance, $r$ is internal resistance and ${{R}_{eq}}$ is effective resistance of the circuit.

Complete step by step solution:
To answer the given question, let first derive an expression for the current flowing in a load in the terms of the internal resistance. For this, consider a closed electric circuit, as shown in the figure below.

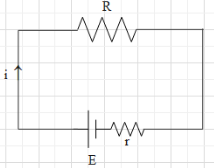
The circuit consists of a battery (an energy source), whose emf is E and a load resistance R in connected to the terminal of the battery. Let the battery have some internal resistance r. We can show the internal resistance of the battery by drawing a resistance r in series with the battery of emf E. The given circuit is a series circuit. Therefore, the same amount of current will flow in all the components. Let the current in the circuit be i. Since the resistances R and r are in series connection, the effective resistance of the two is equal to ${{R}_{eq}}=R+r$.
And from Ohm’s law we know that $E=i{{R}_{eq}}$ ….. (i).
Substitute the value of ${{R}_{eq}}$ in equation (i).
$E=i(R+r)$
$\Rightarrow i=\dfrac{E}{R+r}$.
Therefore, the current in the load resistance can be written as $i=\dfrac{E}{R+r}$ ….. (ii)

Now, if we keep the emf of the battery and the resistance of the load constant, then the current in the load will depend on the internal resistance of the battery. From equation (ii), we understand that if we increase the value of r, the denominator will increase. As a result the value of i will decrease. And if we decrease the value of the r, the value of i will increase.This means that for a maximum current in the load, the value of the internal resistance must be minimum and the minimum value of r is zero. Therefore, an energy source will supply a maximum current into the load if its internal resistance is zero.

Hence, the correct option is A.

Note: When n resistances (${{R}_{1}},{{R}_{2}},{{R}_{3}},.....{{R}_{n}}$) are in series connection, the effective resistance of the this combination is given as, ${{R}_{eq}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.....{{R}_{n}}$.
When $n$ resistances (${{R}_{1}},{{R}_{2}},{{R}_{3}},.....{{R}_{n}}$) are in parallel connection, the effective resistance of the this combination can be written as, $\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.....+\dfrac{1}{{{R}_{n}}}$.