Question

An element \['X'\] has a valency of \[H\]. Write its formula for carbonate?

Answer 1

Hint: To solve this question one must have the basic knowledge of chemical bonding in chemistry. With the help of basic knowledge of chemical bonding and the valency of elements, we will be able to develop the formula for carbonate. We have an element \['X'\] with the given valency we will satisfy the valency of carbonate to develop the complete formula.

Complete step by step answer:
First, we will understand the term ‘Valency’ given in the question. The term ‘Valency’ is defined as the combining power of an element. It is simply related to the number of electrons in the outer shell.
Now we are all set to solve the question. In the question, we have the valency of the element \['X'\] as \[H\]. The valency of \[H\] is equal to \[1\]. According to the question, we can conclude that the valency of an element \[X\] equals to \[1\] .
Now we will go back to basics which means we will focus on the definition of ‘Valency’ which is the combining power of elements. So now we will combine the element \[X\] with carbonate \[CO_3^{2 - }\].
Now we have a valency of \[X = 1,\] and valency of carbonate \[CO_3^{2 - } = 2\]. Now to find the formula we will use the basics of valency.

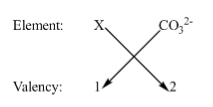
Using the basics of valency we can obtain the formula as \[{X_2}\left( {C{O_3}} \right)\]. The formula is satisfying the valency of both the elements. For example, \[2X\] are required to satisfy the valency of carbonates.

Therefore, the final formula obtained is \[{X_2}\left( {C{O_3}} \right)\].

Note:
There is one method to find the valency of elements. If the number of electrons in the outermost shell is less than \[4\] , then the compound is said to have positive valency. Above \[4\] the valency is obtained by subtracting the electron from eight.