Question

An element A crystalizes in a Fcc structure. $200g$ of this element has $4.12 \times {10^{24}}$ atoms. The density of A is $7.2\,gc{m^{ - 3}}$ . Calculate the edge length of the unit cell.
A.\[26.97 \times {10^{ - 24}}cm\]
B.$299.9\,pm$
C.$5 \times {10^{ - 12}}\,cm$
D.$2.99\,cm$

Answer 1

Hint: The formula for finding density is $\dfrac{{Z \times M}}{{{a^3} \times {N_0} \times {{10}^{ - 30}}}}$. On substituting the values, we will get the desired result.

Complete step by step answer:
We know that, Density = $\dfrac{{Z \times M}}{{{a^3} \times {N_0} \times {{10}^{ - 30}}}}$
For hcp and fcc structure, we will take Z=$4$

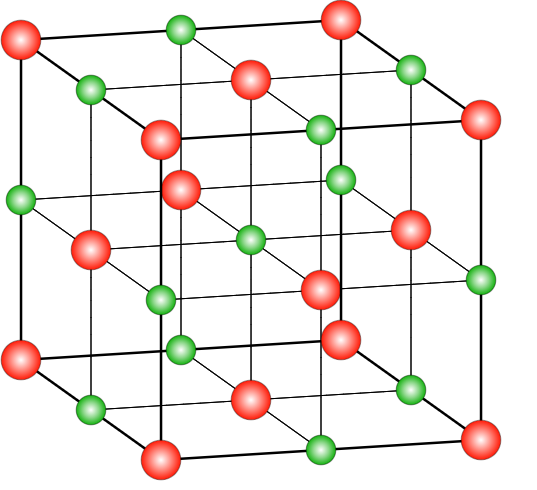
Diagram showing FCC structure
So, According to question,
Density is given as $7.2\,gc{m^{ - 3}}$
Mass given = $200g$
Atomic mass (M) of the element is calculated as:
In $200g$ , $4.12 \times {10^{24}}$ atoms of the element are present
$6.022 \times {10^{23}}$ atoms of the element are present in
$ = \,\dfrac{{200g}}{{4.12 \times {{10}^{24}}}}\, \times \,6.022 \times {10^{23}}\, = \,29.23g$
Atomic Mass (M) of the element = $29.23\,g\,mo{l^{ - 1}}$
Value of Avogadro’s Number (${N_0}$) = \[6.022 \times {10^{23\,}}mol{e^{ - 1}}\]
On substituting the values,
\[{a^3}\, = \,\dfrac{{4 \times 29.23}}{{7.2 \times 6.022 \times {{10}^{23}} \times {{10}^{ - 30}}}}\]
$ = \,26.97 \times {10^6}\,{(pm)^3}$
Edge Length (a) = \[{[26.97 \times {10^6}\,{(pm)^3}]^{\dfrac{1}{3}}}\, = \,2.999\, \times \,{10^2}\,pm{\kern 1pt} \, = \,299.9\,pm\]
Therefore, option A, C and D are incorrect.
Hence, the correct answer is $2.99\,cm$ which is option B.

Note:
For BCC, Z = $2$
For HCP, Z = $4$
In the Face Centered Cubic arrangement, there is one atom centered in each of the faces and eight atoms at corners of the unit cell. The atom in the face is shared with the adjacent cell. FCC unit cells consist of four atoms, eight eighths at the corners and six halves in the faces.
The body-centered cubic unit cell has atoms at each of the eight corners of a cube (like the cubic unit cell) plus one atom in the center of the cube. The corner atoms are shared among eight unit cells.