Question

An electron, moving along the x-axis with an initial energy of $100eV$,enters a region of magnetic field $\vec{B}=\left( 1.5\times {{10}^{-3}}T \right)\hat{k}$ at S (See figure). The field extends between $x = 0$ and $x = 2cm$. The electron is detected at the point Q on screen placed $8cm$away from the point. What is the distance $d$ between P and Q (on the screen)?
(electron's charge =$1.6\times {{10}^{-19}}C$, mass of electron =$~9.1\times {{10}^{-3}}kg$)

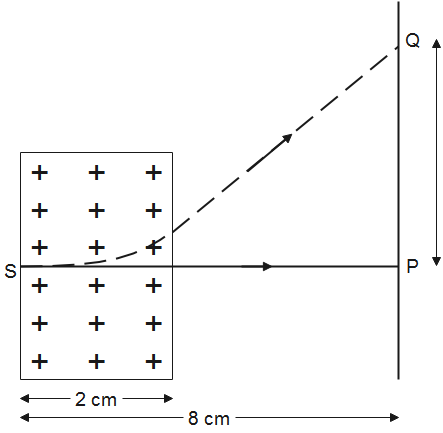
A. 12.85 cm
B. 1.22 cm
C. 11.65 cm
D. 2.25 cm

Answer 1

Hint: In magnetic field, a moving charge experiences force known as magnetic force. As charge moves perpendicular to the magnetic field, the path it follows in the magnetic field is circular. The centripetal force is provided by magnetic force. Find the radius of the circular path and then use geometry to obtain the separation between P and Q.

Complete step by step answer:
When a charge $q$ enters a magnetic field $B$ with velocity $v$, it experiences a force known as magnetic force given by
${{\mathbf{F}}_{m}}=q\left( \mathbf{v}\times \mathbf{B} \right)$
If charge is moving perpendicular to direction of magnetic field, force acts on it tangentially and the path of the charge in the magnetic field is circular. The centripetal force is provided by magnetic force and therefore,
$qvB=\dfrac{m{{v}^{2}}}{R}\Rightarrow R=\dfrac{\sqrt{2m({{E}_{k}})}}{qB}$
Where R is the radius of the circle and ${{E}_{k}}$ is its kinetic energy. In this problem, electron has kinetic energy ${{E}_{k}}=100eV$ enters a region of magnetic field $\vec{B}=\left( 1.5\times {{10}^{-3}}T \right)\hat{k}$. Therefore, radius of the circle
$R=\dfrac{\sqrt{2\times 9.1\times {{10}^{-31}}(100\times 1.6\times {{10}^{-19}})}}{1.6\times {{10}^{-19}}\times 1.5\times {{10}^{-3}}}$
On solving this, we get
$R=2.248cm$
Let us assume that the electron exits at an angle $\theta$ to the horizontal.

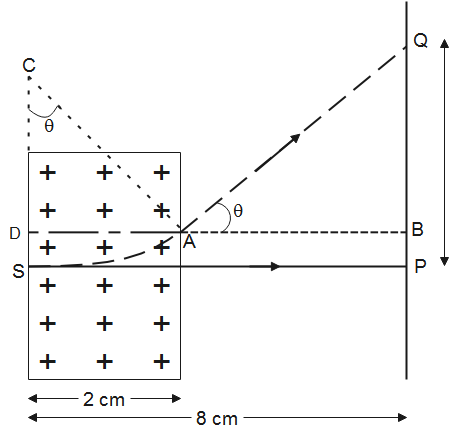
According to trigonometric ratios, in triangle ACD
$\sin \theta =\dfrac{BD}{CB}=\dfrac{2}{2.248}=0.89$
From identity ${{\sin }^{2}}\theta +co{{s}^{2}}\theta =1$, we have
$\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }=\sqrt{1-0.79}=\sqrt{0.21}=0.46$
In triangle ABQ
$\tan \theta =\dfrac{QB}{BA}$
It can be observed that $BA=8cm-2cm=6cm$
Substituting this, we have
$\tan \theta =\dfrac{QB}{6}=\dfrac{\sin \theta }{\cos \theta }$
Substituting the values and rearranging,
$QB=6\times \dfrac{0.89}{0.46}=11.61cm$
Also, $BP=DS=R(1-\cos \theta )=2.248\times 0.54=1.21cm$
$PQ=BP+QB=11.61+1.21=12.82cm$
Therefore, $d=12.82cm$
Which is approximately equal to option A.
Therefore, option A is the correct answer.

Note:
A moving charge experiences a force in a magnetic field known as magnetic force. The direction of force is perpendicular to both the direction of motion and direction of magnetic field. If motion of charge is perpendicular to direction of magnetic field, charge moves in circular path.