Question

An electric lamp and a screen are placed on the table, in a line at a distance of $1m$. In what position of a convex lens of the focal length of $f = 21cm$ will the image of the lamp be sharp?

Answer 1

Hint: A convex lens converges the lights coming from the source. Here the source is the light bulb which is at a fixed distance from the screen. To get a sharp image on the screen, the image should be formed just on the screen. To get it on the screen, the image should be real.

Formula Used:
If a lens has a focal length $f$ and if the object is placed at a distance $u$ and the image is formed at a distance $v$ then the relation is
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$

Complete step by step answer:
Given, the focal length of the lens is $21cm$.
The screen and the bulb have a distance of $1m$ or $100cm$.
To get: The position to get a sharp image of the bulb.

Step 1:

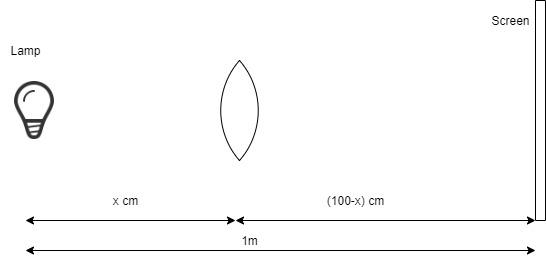
Since the image is real, the screen and the lamp should be on opposite sides of the convex lens.
Let the distance from the object to the lens is $x$ cm.
So, the distance from the lens to the screen is $\left( {100 - x} \right)cm$.

Step 2:
You now have, $u = - xcm$, $v = \left( {100 - x} \right)cm$ and $f = 21cm$
Compute the value of $x$ from the relation in eq (1)
\[
  \dfrac{1}{{21}} = \dfrac{1}{{100 - x}} + \dfrac{1}{x} \\
   \Rightarrow \dfrac{1}{{21}} = \dfrac{{x + 100 - x}}{{100x - {x^2}}} \\
   \Rightarrow 100x - {x^2} = 21x + 2100 - 21x \\
   \Rightarrow {x^2} - 100x - 2100 = 0 \\
   \Rightarrow \left( {x - 30} \right) \times \left( {x - 70} \right) = 0 \\
 \]
Hence, the solutions are $x = 30cm$ or $x = 70cm$ .

The lens should be placed in the middle of the screen at a distance of $30cm$ or $70cm$ from the bulb.

Note:
The distance of the object from the lens in the eq (1) should be negative as the direction of light is different. The image should be real so that it can be projected on the screen, hence the screen and the object should be on the opposite side of the lens. You must be careful in these two points. Then from the relation, you shall get a quadratic equation in this type of problem. Hence, you will have two solutions that you can check for validity with other conditions given.