Question

An electric field is uniform, and in the positive x-direction for positive x, and uniform with the same magnitude, but in the negative x-direction for negative x. It is given that E = 200$\hat i$N/C for x > 0 and E = - 200$\hat i$N/C for x < 0 A right circular cylinder of length 20 cm and radius 5 cm has its centre at the origin and its axis along the x-axis so that one face is at x = +10 cm and other is at x = -10 cm.
(a) What is the net outward flux through each flat face?
(b) What is the flux through the side of the cylinder?
(c) What is the net outward flux through the side of the cylinder?

Answer 1

Hint:The diagram of the cylinder can be drawn following the statements given in the question. To calculate the flux on various surfaces of the cylinder use gauss’s law.

Formula used:
$\oint\limits_S {\overrightarrow E. \overrightarrow {da} } = \dfrac{q}{{{\varepsilon _0}}}$ where, \[\overrightarrow E \]= Electric field
q = Charge
\[\overrightarrow {da} \] = Area vector
and its relationship with flux is:
\[\phi = \oint\limits_S {\overrightarrow E. \overrightarrow {da} } \] where,
$\phi $ = Electric flux.

Complete step by step answer:
The diagram of the cylinder according to the question is:

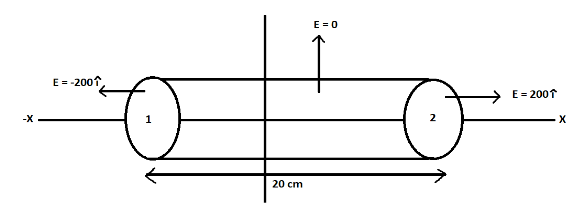
The electric field along the side is 0 because:
$\overrightarrow E. \overrightarrow {da} $= $\left| {\overrightarrow E } \right|\left| {\overrightarrow {da} } \right|\cos \theta $ (dot product)
The angle between the electric field and area vector is 90° and cos 90 is 0, thus the electric field also becomes 0
Given:
\[{\overrightarrow E _1}\]= - 200$\hat i$N/C 🡪 \[\left| {{{\overrightarrow E }_1}} \right|\] = 200
\[{\overrightarrow E _2}\]= 200$\hat i$N/C 🡪 \[\left| {{{\overrightarrow E }_2}} \right|\] = 200
Radius (r) = 5 cm or $\dfrac{5}{{100}}m$ = 0.05 m
Distance between each surface from origin = 10 cm
Collective distance between the two surfaces = 20 cm
Now, according to Gauss’s Law:
The total flux of a closed surface is $\dfrac{1}{{{\varepsilon _0}}}$ times the charge enclosed by it:
$\oint\limits_S {\overrightarrow E. \overrightarrow {da} } = \dfrac{q}{{{\varepsilon _0}}}$ _______ (1)
And electric flux is defined as the rate of change of electric field for a unit area:
\[\phi = \oint\limits_S {\overrightarrow E. \overrightarrow {da} } \] _______ (2)
Answering the questions:
(a) Net outward flux through each flat face:
1 and 2 surfaces in the figure are flat surface, the angle they form with area vector is 0 (since parallel) considering surface (2) to calculate flux:
From (2):
\[\phi = \oint\limits_S {\overrightarrow E. \overrightarrow {da} } \] and From (1):
$\left| {\overrightarrow E } \right|\left| {\overrightarrow {da} } \right|\cos \theta $
Here,
$\theta $ = 0
\[\overrightarrow {\left| E \right|} \]= 200
\[\overrightarrow {\left| {da} \right|} \] = $\pi {r^2}$ (as it is a circular surface)
r = 0.05 (given)
\[\overrightarrow {\left| {da} \right|} \] = $\pi {(0.05)^2}$
Substituting the values:
$\left| {\overrightarrow E } \right|\left| {\overrightarrow {da} } \right|\cos \theta = 200 \times \dfrac{{22}}{7} \times 0.05 \times 0.05$= 1.57
Thus, the net outward flux through each flat face is 1.57 $N{m^2}{C^{ - 1}}$
(b) Flux through the side of the cylinder:
From (2):
\[\phi = \oint\limits_S {\overrightarrow E. \overrightarrow {da} } \] and From (1):
$\left| {\overrightarrow E } \right|\left| {\overrightarrow {da} } \right|\cos \theta $
Here,
$\theta $ = 0
So, \[\overrightarrow {\left| E \right|} \]= 200
$ \Rightarrow \phi = 0$
Thus, flux through the side of the cylinder is 0.
(c) Net outward flux through side of the cylinder:
This flux is due to the surface 1 and 2.
From (1)
\[\phi = \oint\limits_S {\overrightarrow E. \overrightarrow {da} } \]
The magnitude of electric field on both the surface is same (200) and the area of both will also be the same:
\[{\phi _{net}} = 2E.A\cos \theta \]
$\theta = $0 (between electric field and area vector)
$\Rightarrow\cos \theta $ = 1
The net electric field will be:
\[{\phi _{net}} = 2E.A\]
E = 200
A = $\pi {r^2}$ (circular surfaces)
A = $\pi {(0.05)^2}$ [As r = 0.05 m]
Substituting the values:
\[{\phi _{net}} = 2 \times 200 \times \pi \times \dfrac{5}{{100}} \times \dfrac{5}{{100}}\]
\[{\phi _{net}} = \pi \]
$\pi $ = 3.14
\[ \therefore {\phi _{net}} = 3.14\]
Thus, the net outward flux through side of the cylinder is 3.14 $N{m^2}{C^{ - 1}}$.

Note: We use $\left| {} \right|$ to denote the magnitude (value) of a vector
$\oint\limits_S {} $denotes the surface integral of the respective quantity
In general, the electric flux is directly proportional to the number of electric field lines entering the given surface
Dot product and cross product respectively are:
$
a.b = ab\cos \theta \\
\therefore a \times b = ab\sin \theta \\
$