Question

An effort of $50kgf$ is applied at the end of a lever of the second order which supports a load of $750kgf$. Calculate the mechanical advantage of the system.

Answer 1

Hint: The length of the lever will be equivalent to the effort arm. The mechanical advantage can be found by finding the value of the effort arm. That is the product of the value of the effort and the length of the effort arm which will be equivalent to the value of load and length of the load arm. This will help you in answering this question.

Complete answer:
First of all draw the image of the conditions mentioned in the question.

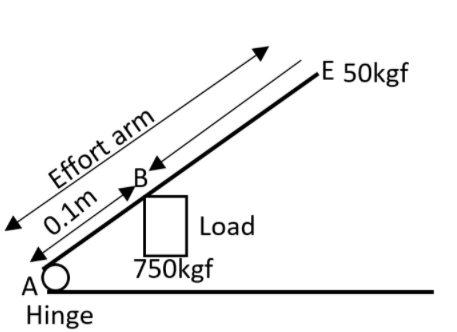
The length of the lever will be equivalent to the effort arm. This can be written as,
$\text{Length of lever}=\text{effort arm}=AE$
The length of the load arm will be equivalent to the length mentioned as AB. The value of this arm will be given as,
$AB=0.1m$
The value of the effort has been mentioned as,
$E=50kgf$
The value of the load has been given as,
$L=750kgf$
The mechanical advantage can be found by finding the value of the effort arm. That is the product of the value of the effort and the length of the effort arm which will be equivalent to the value of load and length of the load arm. This can be expressed in an equation as,
$\text{effort}\times \text{effort arm}=\text{load}\times \text{load arm}$
Substituting the values in it will give,
$AE\times 50=750\times 0.1$
Rearranging the equation can be written as,
$AE=\dfrac{750}{50}\times \dfrac{1}{10}=1.5m$
Therefore the mechanical advantage of the system will be $1.5m$.

Therefore the answer has been calculated.

Note:
Mechanical advantage is defined as the amount of the amplification of the force produced with the help of a mechanical device or machine system. The device will store the input power and provide the forces against movement in order to achieve a required amplification in the output force. Basically mechanical advantage is the ratio of the output force to the input force.