Question

An alternating voltage $v\left( t \right) = 220\sin 100\pi t$ volt voltage is applied to a purely resistance load of $50\Omega $ . The time taken for the current to rise from half of the peak value of the peak value is:
$\left( a \right)\,\,2.2ms$
$\left( b \right)\,\,5ms$
$\left( c \right)\,\,3.3ms$
$\left( d \right)\,\,7.2ms$

Answer 1

Hint: Voltage leads current by or $\dfrac{\pi }{2}$ . The equation of the current will be $I(t) = 220\sin \left( {100\pi t - 90^\circ } \right)$ . Write it in the cosine form. Calculate the phase angle, where the value of cosine will be $\dfrac{1}{2}$ . Equate the $\omega t$ and that angle.
 Formula used: If the angular velocity of a coil is $\omega $ , time period $T$ and phase angle is $2\pi $ , then, $T = \dfrac{{2\pi }}{\omega }$

 Complete step by step answer: Let, at time $t$ , peak value becomes $\dfrac{1}{2}$ . We know that voltage leads current by $90^\circ $ or $\dfrac{\pi }{2}$

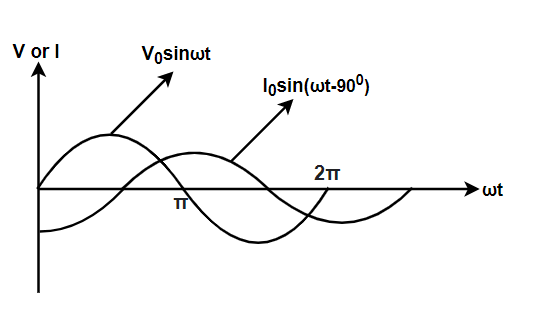
We are given the equation of applied voltage, $v\left( t \right) = 220\sin 100\pi t$ So, the equation of current will be $I(t) = 220\sin \left( {100\pi t - 90^\circ } \right)$ So, the equation of current, in the form of cosine will be $I(t) = 220\cos \left( {100\pi t} \right)$
Also, we know that $\cos 60^\circ = \cos \dfrac{\pi }{3} = \dfrac{1}{2}$
So, the time taken for the current to rise from half of the peak value of the peak value will be at $t = \dfrac{\pi }{3}$
So, $\dfrac{\pi }{3} = 100\pi t$
$ \Rightarrow t = \dfrac{\pi }{{3 \times 100\pi }} = \dfrac{1}{{300}} = 3.3ms$

 Hence, the option $\left( c \right)$ is correct.

 Additional information: The definite time interval in which a complete cycle repeats itself, is called the time period of an alternating current or AC.
If the angular velocity of a coil is $\omega $ , time period $T$ and phase angle is $2\pi $ , then, $T = \dfrac{{2\pi }}{\omega }$
The number of complete waves produced in unit time is called the frequency $\left( n \right)$ of an alternating current. So, $n = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}$ Note that frequency is the most important quantity in the expression of an alternating current.
Also, let the equation of alternating current be $i = {i_0}\sin \left( {\omega t + \alpha } \right)$ Now, the state of alternating current at any moment is expressed by its phase. In the above equation of the alternating current $\left( {\omega t + \alpha } \right)$ is the phase of the alternating current.

 Note: For the equation $i = {i_0}\sin \left( {\omega t + \alpha } \right)$ and $v = {v_0}\sin \left( {\omega t + \alpha } \right)$ , as $ - 1 \leqslant \sin \theta \leqslant 1$ , we can say that the maximum and minimum values of emf ${v_0}$ and $ - {v_0}$ respectively. Also, the maximum and minimum values of the currents are ${i_0}$ and $ - {i_0}$ respectively. These magnitudes, ${v_0}$ and ${i_0}$ are the peak values of the emf and current. Also, it should be noted that the peak value of current varies inversely with the resistance of the circuit.