Question

An alternating current source E = 100 sin (1000t) volt is connected through an inductor of $10\mu H$ then writes down the equation of current.

Answer 1

Hint: We can compare the given value of voltage with \[E = {E_o}\sin \omega t\] to obtain certain values which will be substituted in the equation for current so as to get the required equation. The inductor present in this question will provide the resistance to the flowing current.

Formulas used:
V = IR (ohm’s law) where V is voltage, I and R are current and resistance respectively.
${X_L} = \omega L$ 🡪 Inductive reactance (resistance) of the conductor
For conversion, remember:
${10^6}\mu H = 1H$

Complete step by step answer:
In alternating current, we can write voltage as currents as:
\[E = {E_o}\sin \omega t\] __________ (1)
And
\[I = {I_o}\sin \omega t\] __________ (2)
Where ${E_o}$ and ${I_o}$ are the maximum values of voltage and current respectively.
Now, the given value of voltage is:
E = 100 sin (1000t)
Comparing this with equation (1):
${E_o}$ = 100 _______ (3)
$\omega $ = 1000 _______ (4)
The inductor that is connected provide some resistance (called inductive reactance) to the flowing current which is given as:
${X_L} = \omega L$
L = Inductance
L = $10\mu H$ (given)
$\Rightarrow$ L = $\left( {10 \times {{10}^{ - 6}}} \right)H$ $\left( {\because {{10}^6}\mu H = 1H} \right)$
And
$\omega $ = 1000 [from (4)]
Substituting:
$
  {X_L} = 1000\left( {10 \times {{10}^{ - 6}}} \right) \\
  {X_L} = {10^{ - 2}} \\
 $
From ohm’s law:
V = IR
For I, it can be written as:
$I = \dfrac{V}{R}$
Here,
Voltage (V) = ${E_o}$
Resistance (R) = ${X_L}$
Current (I) = ${I_o}$ (because when voltage is maximum, current will also be maximum)
$ \Rightarrow {I_o} = \dfrac{{{E_o}}}{{{X_L}}}$
Substituting the values, we get:
$
  {I_o} = \dfrac{{100}}{{{{10}^{ - 2}}}} \\
\Rightarrow {I_o} = 100 \times 100 \\
\Rightarrow {I_o} = 10000 \\
 $
Substituting all the known values in eqn (2) to get the required equation of current:
\[
  I = {I_o}\sin \omega t \\
  I = 10000\sin 1000t \\
 \]
Since $\omega $ = 1000 [from (4)]
Therefore the required equation of current is:
\[I = 10000\sin 1000t\].

Note:
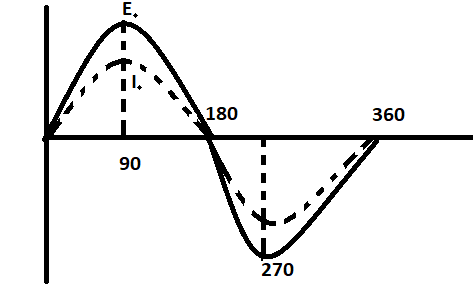
Both ${I_o}$ and ${E_o}$ lies in the same phase, they both are functions of sin (as sign by the equations), the Phasor diagram to depict their relationship can be given as: