Question

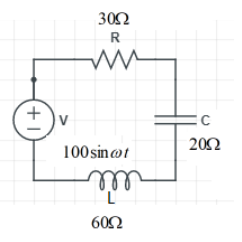
An altering voltage $V=100sin\omega t$ is applied across an LCR circuit as shown. At the instant when voltage is drop across source is $50\sqrt3V$, then at that instant

A. voltage drop across inductor is $120cos7^{\circ}V$
B. voltage drop across capacitor is $40cos173^{\circ}V$
C. voltage drop across resistor is $60cos7^{\circ}V$
D. All of the above

Answer 1

Hint: A LCR circuit is where the inductor $L$ , capacitance $C$ and resistance $R$ are connected to an AC source. Here the LCR is connected in series circuit. Then the phase difference between the current and the voltage is $90^{\circ}$
Formula: $cos \phi=\dfrac{R}{Z}$,$i=\dfrac{Vsin(\omega t-\phi)}{Z}$

Complete answer:
We know that the source of an AC circuit is sinusoidal. Then there is a phase difference between the voltage and current. If the phase difference between the current and voltage is zero, then both are said to be in phase, and if the phase difference is not equal to zero, then both are said to be out of phase.
Here, given that the input voltage $V=100sin\omega t$, $L=X_{L}=60\Omega$, $R=30\Omega$ and $C=X_{C}=20\Omega$
Given that at some instant $t$ the voltage drop becomes $V=50\sqrt3$
Then, at some instant $t$, $V=100sin\omega t=50\sqrt3$
$\implies sin\omega t=\dfrac{50\sqrt 3}{100}=\dfrac{\sqrt3}{2}$
But $sin 60=\dfrac{\sqrt3}{2}$
$\implies \omega t=60^{\circ}$
Since the circuit is in series connection, we know that the current in the circuit remains the same, and then the current in the circuit is given as $i=\dfrac{V}{Z}$
Where $Z$ is the impedance of the circuit or the total resistance offered by the circuit, it is given as$Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}$. Here $X_{L},X_{C}$ are the inductive reactance and the capacitive reactance.
Then substituting the values, we get, $Z=\sqrt{30^{2}+(60-20)^{2}}=\sqrt{900+1600}=\sqrt{2500}=50$
Also the phase difference $cos \phi=\dfrac{R}{Z}=\dfrac{30}{50}=\dfrac{3}{5}$
$\implies \phi=53^{\circ}$
Here since$X_{L}>X_{C}$, we can say that the voltage leads current by $\phi$
Then the current in the circuit $i=\dfrac{Vsin(\omega t-\phi)}{Z}=\dfrac{100 sin(60-53)}{50}=2sin7^{\circ}$
Then the potential drop across the resistor at $t$ is given as,$V_{R}=iR=30 \times 2sin7^{\circ}=60sin7^{\circ}$, the voltage lags current by $90^{\circ}$, then $60sin(90-7)=60cos7^{\circ}$
In inductor, the voltage lags current by $90^{\circ}$, then $V_{I}=iX_{L}=60\times 2sin(90-7^{\circ})=120cos(7^{\circ})$
Similarly, in the capacitor, the voltage lags current by $180^{\circ}$, with respect to $V$, then $V_{C}=iX_{C}=20\times 2sin(180-7^{\circ})=40cos(173^{\circ})$

Thus the answer is option D. All of the above

Note:
Resonance is observed when RLC is connected in series; here there is no phase difference between the current and the voltage. For frequency less than the resonant frequency, the impedance is capacitive in nature and for frequency greater than the resonant frequency; the impedance is inductive in nature.