
An $\alpha $ particle having energy $10MeV$ collides with a nucleus of atomic number 50. Then distance of closest approach will be
$\begin{align}
& \text{A}\text{. }14.4\times {{10}^{-16}}m \\
& \text{B}\text{. }1.7\times {{10}^{-7}}m \\
& \text{C}\text{. }1.4\times {{10}^{-12}}m \\
& \text{D}\text{. }14.4\times {{10}^{-15}}m \\
\end{align}$
Answer
589.5k+ views
- Hint: The scattering of an alpha particle through a large angle with respect to its original direction of motion is caused by an atom whose most of the mass and all of the positive electric charge is being concentrated at the center or the nucleus of the atom. In this collision between the alpha particle and the atom, we define a term known as distance of closest approach, which is the distance between the centres of the alpha particle and the atom. At the distance of closest approach, the kinetic energy of the alpha particle is converted into its potential energy.
Complete step-by-step solution
The distance of the closest approach of two particles is defined as the distance between their centers when the particles are externally tangent to each other. The objects can be exact geometric shapes or physical particles with well-defined boundaries. The distance of closest approach is also called the contact distance.
For the simplest objects, such as spheres, the distance of closest approach is the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects in the space.
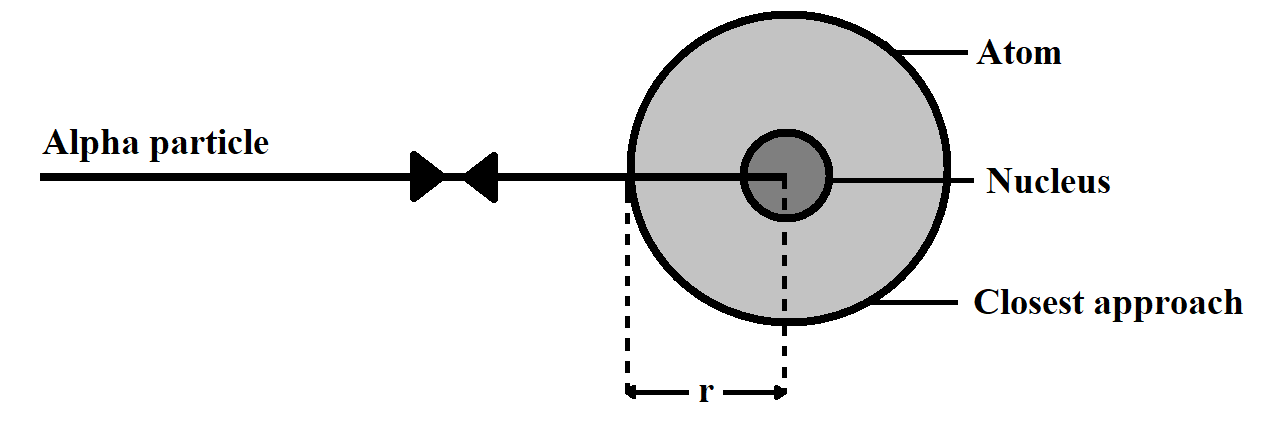
At the distance of closest approach, the whole kinetic energy of the particle gets converted into potential energy.
Therefore,
$KE=\dfrac{1}{4\pi {{\varepsilon }_{o}}}\dfrac{2Z{{e}^{2}}}{r}$
Where,
$Z$ is the atomic number
$e$ is the charge on an electron
$r$ is the distance of closest approach
Putting values,
$\begin{align}
& KE=10\times 1.6\times {{10}^{-13}} \\
& \dfrac{1}{4\pi {{\varepsilon }_{o}}}=9\times {{10}^{9}} \\
& Z=50 \\
& e=1.6\times {{10}^{-19}} \\
\end{align}$
We get,
$\begin{align}
& 10\times 1.6\times {{10}^{-13}}=9\times {{10}^{9}}\times \dfrac{2\times 50\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{r} \\
& r=\dfrac{9\times {{10}^{9}}\times 2\times 50\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{10\times 1.6\times {{10}^{-13}}} \\
& r=14.4\times {{10}^{-15}}m \\
\end{align}$
The distance of closest approach is $14.4\times {{10}^{-15}}m$
Hence, the correct option is D.
Note: Students should note the key difference between the distance of closest approach and the impact meter. Distance of closest approach is the distance between the centre of nucleus and the point from which the alpha particle, which is approaching directly to the nucleus, returns, while Impact parameter is expressed as the perpendicular distance of the velocity vector of the alpha particle from the central line of the nucleus; when the particle is far away from the atom.
Distance of closest approach is expressed as $r$ Impact parameter is expressed as $b$.
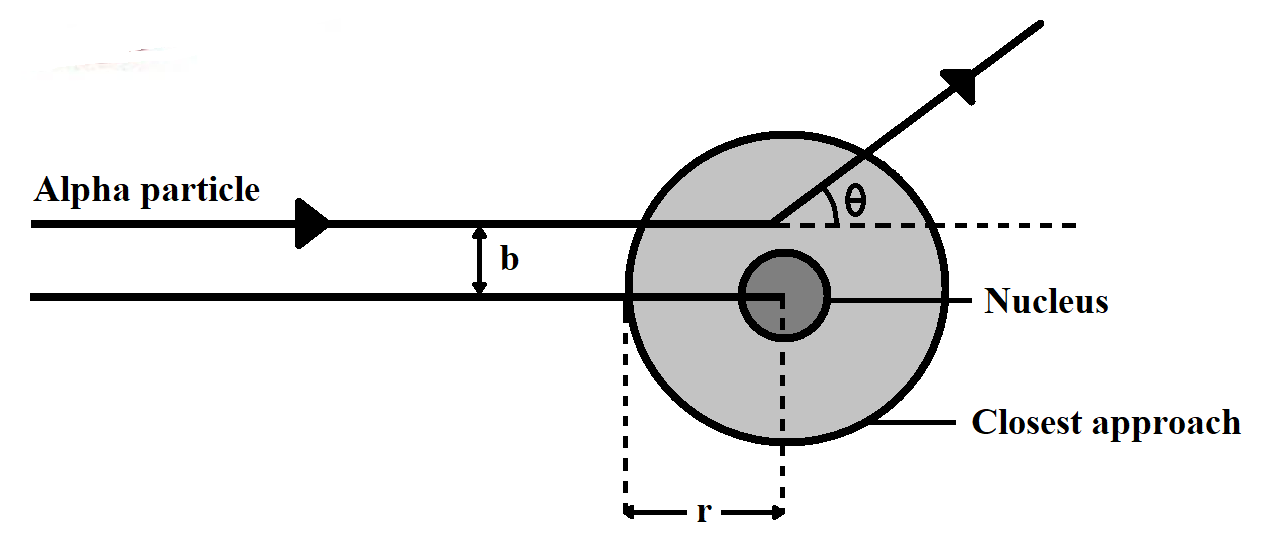
Complete step-by-step solution
The distance of the closest approach of two particles is defined as the distance between their centers when the particles are externally tangent to each other. The objects can be exact geometric shapes or physical particles with well-defined boundaries. The distance of closest approach is also called the contact distance.
For the simplest objects, such as spheres, the distance of closest approach is the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects in the space.

At the distance of closest approach, the whole kinetic energy of the particle gets converted into potential energy.
Therefore,
$KE=\dfrac{1}{4\pi {{\varepsilon }_{o}}}\dfrac{2Z{{e}^{2}}}{r}$
Where,
$Z$ is the atomic number
$e$ is the charge on an electron
$r$ is the distance of closest approach
Putting values,
$\begin{align}
& KE=10\times 1.6\times {{10}^{-13}} \\
& \dfrac{1}{4\pi {{\varepsilon }_{o}}}=9\times {{10}^{9}} \\
& Z=50 \\
& e=1.6\times {{10}^{-19}} \\
\end{align}$
We get,
$\begin{align}
& 10\times 1.6\times {{10}^{-13}}=9\times {{10}^{9}}\times \dfrac{2\times 50\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{r} \\
& r=\dfrac{9\times {{10}^{9}}\times 2\times 50\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{10\times 1.6\times {{10}^{-13}}} \\
& r=14.4\times {{10}^{-15}}m \\
\end{align}$
The distance of closest approach is $14.4\times {{10}^{-15}}m$
Hence, the correct option is D.
Note: Students should note the key difference between the distance of closest approach and the impact meter. Distance of closest approach is the distance between the centre of nucleus and the point from which the alpha particle, which is approaching directly to the nucleus, returns, while Impact parameter is expressed as the perpendicular distance of the velocity vector of the alpha particle from the central line of the nucleus; when the particle is far away from the atom.
Distance of closest approach is expressed as $r$ Impact parameter is expressed as $b$.

Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




