Question

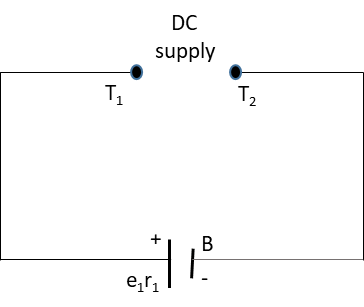
An accumulator battery (storage cell) B of emf E and internal resistance r is being charged from a DC supply whose terminals are \[{T_1}\] and \[{T_2}\]:

A. potential difference between \[{T_1}\] and \[{T_2}\]must be \[ > E\]
B.\[{T_1}\] must be positive with respect to \[{T_2}\]
C. in the battery, current flows from the positive to the negative terminal
D. all the above options are correct

Answer 1

Hint: Use the concept that for the charging of a battery, the potential of the supply should be greater than the total potential of the battery. Determine the expression for the potential difference between the terminals of the DC supply and check the potential of the terminals of the supply and the direction of current flow from the terminals of the battery.

Complete step by step answer:
We have given that an accumulator battery (storage cell) B of emf E and internal resistance r is being charged from a DC supply whose terminals are \[{T_1}\] and \[{T_2}\].
For the DC supply to charge the accumulator battery, the potential of the DC supply should be greater than the emf E of the battery.
If the potential of the DC supply is greater than the emf E of the battery then only the accumulator battery will get charged and if the potential of the DC supply is less than the emf of the battery then it will be the situation like the accumulator battery is charging the DC supply which is not correct and acceptable.
Hence, the first statement is correct.
The potential difference across the DC supply is equal to the emf \[E\] of the Battery and the potential difference \[Ir\] across the internal resistance.
\[{V_{{T_1}}} - {V_{{T_2}}} = E + Ir\]
The value of the term \[E + Ir\] is positive. Hence, the value of the potential \[{V_{{T_1}}}\] across the terminal \[{T_1}\] is greater than the value \[{V_{{T_2}}}\] across the terminal \[{T_2}\].
Hence, the terminal \[{T_1}\] is positive with respect to the terminal \[{T_2}\].
Hence, the statement B is also correct.
Since the potential of the terminal \[{T_1}\] is positive with respect to the potential of the terminal \[{T_2}\]. For this condition to hold well, the current must flow from the positive terminal to the negative terminal of the battery.
Hence, the statement C is also correct.
Since the statements A, B and C are correct,

Hence the correct option is D.

Note:
During charging of battery is $V = E + Ir$ and during discharging of battery $E = V + Ir$ and emf is equal to potential difference if internal resistance of battery is zero. The students may wonder if the values of the emf and internal resistance of the battery are not given then how one can determine the term \[E + Ir\] is positive. As there is addition of the two terms, the final addition must be positive though it has a very small value.