Question

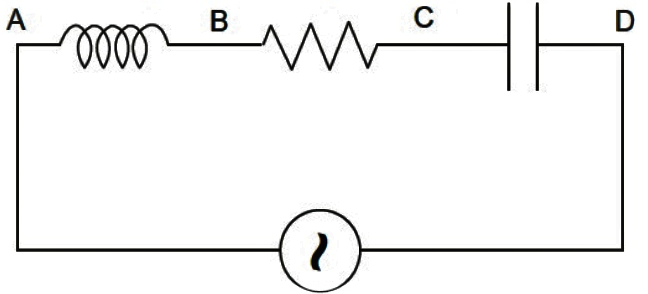
An AC voltmeter connected between points A and B in the circuit below reads 36V. If it is connected between A and C, the reading is 39V. The reading when it is connected between B and D is 25V. What will the voltmeter read when it is connected between A and D? (Assume that the voltmeter reads true rms voltage values and that the source generated a pure AC.)
 

$\begin{align}
  & (A)\sqrt{481}V \\
 & (B)31V \\
 & (C)61V \\
 & (D)\sqrt{3361}V \\
\end{align}$

Answer 1

Hint: The net rms potential across A and D will be due to the root sum of squares of, voltage drop across the resistance and the difference in the voltage drop between the inductor and capacitor. This difference in potential is because when connected in series, the inductor and capacitor are always out of phase with respect to each other.

Complete answer:
Let us first assign some terms that we are going to use later in our solution. Let the voltage drop across the resistance be given by ${{V}_{R}}$, the voltage drop across the capacitance by ${{V}_{C}}$ and finally, the voltage drop across the inductor be ${{V}_{L}}$ .
Then, according to the question, we have:
$\Rightarrow {{({{V}_{L}})}^{2}}={{36}^{2}}$
And,
$\Rightarrow {{V}_{L}}^{2}+{{V}_{R}}^{2}={{39}^{2}}$
Then, using the above equation, we can calculate the voltage drop across the resistance as:
$\begin{align}
  & \Rightarrow {{V}_{R}}^{2}={{39}^{2}}-{{36}^{2}} \\
 & \therefore {{V}_{R}}=15V \\
\end{align}$
It has also been given in the problem that:
$\begin{align}
  & \Rightarrow {{V}_{L}}^{2}+{{V}_{C}}^{2}={{25}^{2}} \\
 & \Rightarrow {{V}_{C}}^{2}={{25}^{2}}-{{15}^{2}} \\
 & \therefore {{V}_{C}}=20V \\
\end{align}$
Now that, we have the potential drop across each component of the circuit, thus we can calculate the potential drop across all of them as:
$\Rightarrow {{V}_{AD}}=\sqrt{\left( {{V}_{R}}^{2} \right)+{{\left| {{V}_{L}}-{{V}_{C}} \right|}^{2}}}$
Putting the values of all the terms in the right-hand side of the equation, we get:
$\begin{align}
  & \Rightarrow {{V}_{AD}}=\sqrt{{{15}^{2}}+{{(36-20)}^{2}}} \\
 & \Rightarrow {{V}_{AD}}=\sqrt{225+256} \\
 & \therefore {{V}_{AD}}=\sqrt{481}V \\
\end{align}$
Hence, the voltage drop or the reading in the voltmeter when it is connected cross AD will be $\sqrt{481}V$.

Hence, option (A) is the correct option.

Note:
A capacitor and inductor are always out of phase, that is, they have a phase difference of ${{180}^{0}}$ when connected in series, and the phase difference of resistor lies in between them. This is the reason why in our final equation we wrote the square of voltage of the resistor term separately from the other two.