
Along solenoid $ S $ has $ n $ turns per meter, with the diameter a. At the center of this coil, we place a smaller coil of $ N $ turns and diameter b (b(A)
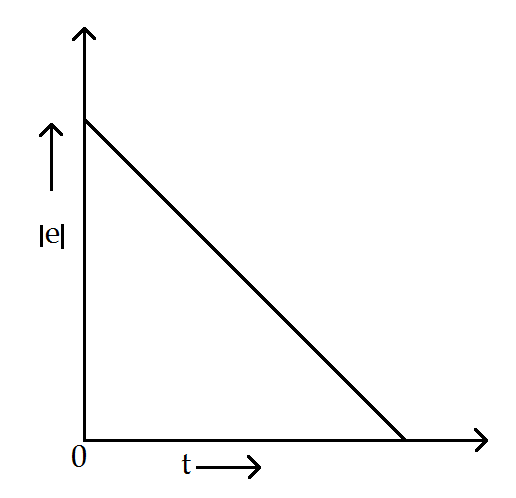
(B)
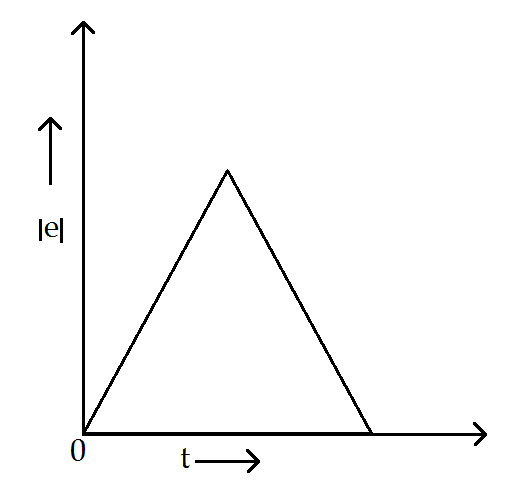
(C)
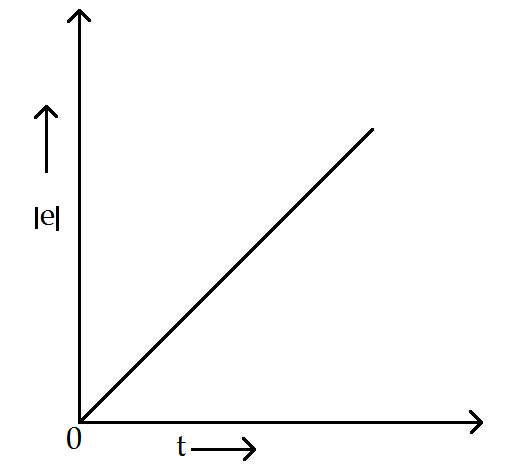
(D)
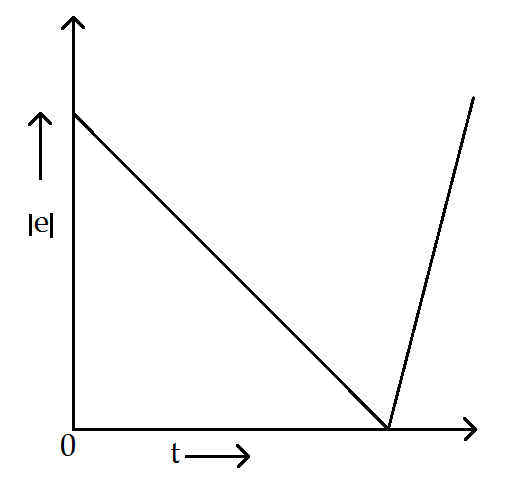

(B)

(C)

(D)

Answer
527.1k+ views
Hint: Here we have given a long solenoid in which another smaller coil is inserted at the center. As we passes current in long solenoid there will be magnetic field established and due to mutual inductance, an induced emf will be produced in the smaller coil which will oppose the current in the solenoid S. So, first we will write down all the given data and then try to establish a relationship between emf and time t to get our final answer.
Complete step by step answer:
Given there is a long solenoid which has diameter ‘a’ and consists of ‘n’ number of turns. In this long solenoid we have inserted another smaller coil with an ‘N’ number of turns and diameter ‘b’ (bThe magnetic field produced due to the current in the solenoid S is given by
$ B={{\mu }_{0}}nI $ ……..(1)
where, $ {{\mu }_{0}} $ is the permeability in free space.
Now, magnetic flux linked with the smaller coil is due to the magnetic field B will be
$ \phi =NBA $ ……...(2)
where, A is an area of a smaller coil. As we know that the radius of the coil is b, therefore the area of the coil will be $ \pi {{b}^{2}} $ . We can rewrite equation 2 as
$ \phi =NB\pi {{b}^{2}} $ …….(3)
Emf induced in the coil is given as rate of change of flux with respect to time. So we have
$ e=-\dfrac{d\phi }{dt} $
where, negative sign indicates that emf induced will oppose the main current in the larger solenoid.
From, equation (3), we have
$e=-\dfrac{d(NB\pi {{b}^{2}})}{dt} \\ $
$\Rightarrow e=-N\pi {{b}^{2}}\dfrac{dB}{dt} \\ $
Substituting value of B from equation (1), we have
$ e=-N\pi {{b}^{2}}\dfrac{d({{\mu }_{0}}nI)}{dt} \\ $
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}\dfrac{dI}{dt} \\ $
As per question, current I varies with t as a function of $ (m{{t}^{2}}+C) $ , therefore above equation becomes
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}\dfrac{d(m{{t}^{2}}+C)}{dt} \\ $
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}(2mt) \\ $
$\Rightarrow e=-2Nnm\pi {{\mu }_{0}}{{b}^{2}}t \\ $
Hence, we conclude that $ |e|\propto t $ , i.e. emf induced will increase linearly with respect to time and the graph between emf and time is given as follows
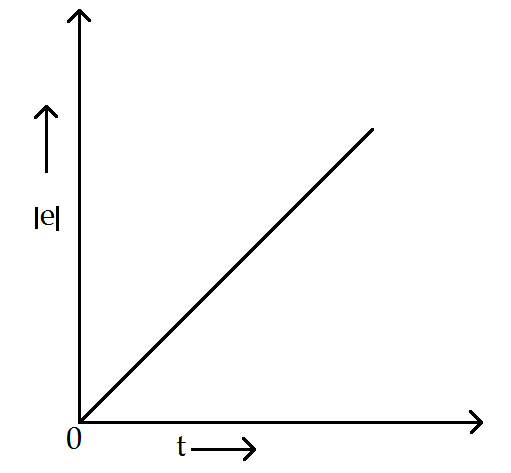
Therefore, option (C) is the correct answer.
Note:
In such a type of question we have to first analyse and then use the concepts like here we use the mutual inductance concept and the main formula was of induced emf. Negative signs can also create confusion but it only represents the opposite change. Also in this question we have given various constants which we can neglect and directly solve the question using proportionality.
Complete step by step answer:
Given there is a long solenoid which has diameter ‘a’ and consists of ‘n’ number of turns. In this long solenoid we have inserted another smaller coil with an ‘N’ number of turns and diameter ‘b’ (b
$ B={{\mu }_{0}}nI $ ……..(1)
where, $ {{\mu }_{0}} $ is the permeability in free space.
Now, magnetic flux linked with the smaller coil is due to the magnetic field B will be
$ \phi =NBA $ ……...(2)
where, A is an area of a smaller coil. As we know that the radius of the coil is b, therefore the area of the coil will be $ \pi {{b}^{2}} $ . We can rewrite equation 2 as
$ \phi =NB\pi {{b}^{2}} $ …….(3)
Emf induced in the coil is given as rate of change of flux with respect to time. So we have
$ e=-\dfrac{d\phi }{dt} $
where, negative sign indicates that emf induced will oppose the main current in the larger solenoid.
From, equation (3), we have
$e=-\dfrac{d(NB\pi {{b}^{2}})}{dt} \\ $
$\Rightarrow e=-N\pi {{b}^{2}}\dfrac{dB}{dt} \\ $
Substituting value of B from equation (1), we have
$ e=-N\pi {{b}^{2}}\dfrac{d({{\mu }_{0}}nI)}{dt} \\ $
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}\dfrac{dI}{dt} \\ $
As per question, current I varies with t as a function of $ (m{{t}^{2}}+C) $ , therefore above equation becomes
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}\dfrac{d(m{{t}^{2}}+C)}{dt} \\ $
$\Rightarrow e=-Nn\pi {{\mu }_{0}}{{b}^{2}}(2mt) \\ $
$\Rightarrow e=-2Nnm\pi {{\mu }_{0}}{{b}^{2}}t \\ $
Hence, we conclude that $ |e|\propto t $ , i.e. emf induced will increase linearly with respect to time and the graph between emf and time is given as follows

Therefore, option (C) is the correct answer.
Note:
In such a type of question we have to first analyse and then use the concepts like here we use the mutual inductance concept and the main formula was of induced emf. Negative signs can also create confusion but it only represents the opposite change. Also in this question we have given various constants which we can neglect and directly solve the question using proportionality.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




