Question

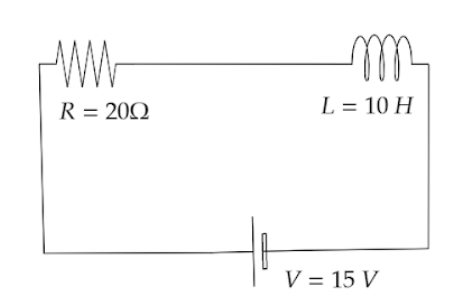
After what time will the PD across the inductor fall to $37\% $ of its initial value.
(1) $\dfrac{1}{3}\,s$
(2) $\dfrac{1}{2}\,s$
(3) $\dfrac{1}{4}\,s$
(4) $\dfrac{3}{4}\,s$

Answer 1

Hint: First of all we have to find the relation between the potential difference of the given circuit with the inductor in charging condition. After that we will make an equation, which by simplifying we will get the time. As this is a LR circuit it has voltage drop across resistor and inductor.

Complete step by step solution:
Let the emf of the battery be $V$.
The potential drop across inductor $L$is ${V_L} = L\dfrac{{dI}}{{dt}}$ and across resistor $R$ is ${V_R} = IR$.
Now from Kirchhoff’s Law we get the total potential difference $V = {V_L} + {V_R}$.
Therefore we get,
$V = L\dfrac{{dI}}{{dt}} + IR - - - - - - \left( 1 \right)$
Arranging the equation we get,
$\dfrac{{V - IR}}{L} = \dfrac{{dI}}{{dt}}$
Dividing the left side by $R$ we get,
$
  \dfrac{{\dfrac{V}{R} - I}}{{\dfrac{L}{R}}} = \dfrac{{dI}}{{dt}} \\
   \Rightarrow \dfrac{{dt}}{{\dfrac{L}{R}}} = \dfrac{{dI}}{{\dfrac{V}{R} - I}} \\
 $
Changing the signs we get,
$ - \dfrac{{dt}}{{\dfrac{L}{R}}} = \dfrac{{dI}}{{I - \dfrac{V}{R}}}$
Integrating both sides with limits of $I$ from $0 - I$ and time from$t - 0$ we get,
$ - \int_0^t {\dfrac{{dt}}{{\dfrac{L}{R}}}} = \int_0^I {\dfrac{{dI}}{{I - \dfrac{V}{R}}}} $
Now by solving it we get,
$ - t\dfrac{L}{R} = \ln \left( {\dfrac{{I - \dfrac{V}{R}}}{{ - \dfrac{V}{R}}}} \right)$
Removing $\ln $ we get,
${e^{ - \dfrac{{tL}}{R}}} = 1 - \dfrac{{IR}}{V}$
$ \Rightarrow I = \dfrac{V}{R}\left( {1 - {e^{ - \dfrac{{tL}}{R}}}} \right) - - - - - \left( 2 \right)$
So we have found the relationship.
Let us consider the potential difference across the LR circuit be ${V_0}$. Thus, we have the relation $I = \dfrac{{{V_0}}}{R}$
 Now, when ${V_0} = 0.37V$ then $t = ?$
Given in the question, $V = 15$, $L = 10$ and $R = 20$.
Substituting all the values in equation $\left( 2 \right)$ we get,
$\dfrac{{0.37V}}{{20}} = \dfrac{V}{{20}}\left( {1 - {e^{ - \dfrac{{tL}}{R}}}} \right)$
We just simplify the power of $e$ term here, $ - \dfrac{{tL}}{R} = - \dfrac{t}{2}$
Now we get,
$0.37 = 1 - {e^{ - \dfrac{t}{2}}}$
$ \Rightarrow 0.63 = {e^{ - \dfrac{t}{2}}}$
Substituting $\log $ in both sides we get,
$
  \log \left( {0.63} \right) = - \dfrac{t}{2} \\
   \Rightarrow - 0.2 \times 2 = - t \\
 $
Thus, by converting into fraction we get,
$t = 0.4 = \dfrac{2}{5}$
Neither option is correct.


Note: It must be noted that when the circuit is open the potential difference of battery is considered to be zero. In this condition we have found the relation in charging action as the diagram given in the question is a closed circuit. When the circuit is closed for a long period of time then the inductor behaves as a conducting wire of zero resistance.