Question

After some time, the rod will approach a terminal speed. Find an expression for it.

$\text{A}\text{. }\dfrac{3E}{2Bl}$
$\text{B}\text{. }\dfrac{E}{2Bl}$
$\text{C}\text{. }\dfrac{E}{Bl}$
$\text{D}\text{. }\dfrac{2E}{Bl}$
$\text{E}\text{. none}$

Answer 1

Hint: Initially there will be a current flowing in the circuit. Then due to this current, the magnetic field will apply a force on the rod and so the rod will accelerate. Then due to this motion of rod there is change in flux and an emf is induced in the circuit. Find an expression for the force exerted on the rod and then you can find the terminal velocity.

Formula used:
$i=\dfrac{E}{R}$
$F=i\left( \overrightarrow{l}\times \overrightarrow{B} \right)$
$\phi =BA$
F=ma
$a=\dfrac{dv}{dt}$

Complete step-by-step answer:
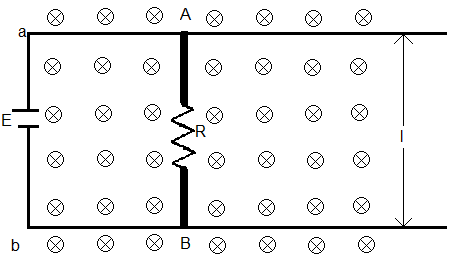
The loop aABb acts as a complete circuit. And since the rod has a resistance of R, a current will flow in the circuit. Let this current be i. By using Ohm’ s law, E=iR.
Therefore, $i=\dfrac{E}{R}$ ….. (i).
When the current i flows through the rod, it acts as a current carrying conductor. When a current carrying conductor is in an external magnetic field B, a force is exerted on the rod, which is equal to $F=i\left( \overrightarrow{l}\times \overrightarrow{B} \right)$,
where l is the length of the conductor and the direction of l is along the direction of current flowing in it.
Hence, in this case also a force F will be exerted on the rod, whose magnitude is $ilB\sin \theta $, where $\theta $ is the angle between $\overrightarrow{B}$ and $\overrightarrow{l}$.
Since, here l and B are perpendicular, $\theta =\dfrac{\pi }{2}$.
Hence, $\sin \theta =1$.
Therefore, $F=ilB$ ….. (ii).
Substitute the value of I from (i) in the above equation.
$F=\dfrac{E}{R}lB$.
According to the left hand Fleming rule, the direction of F will towards right as shown.

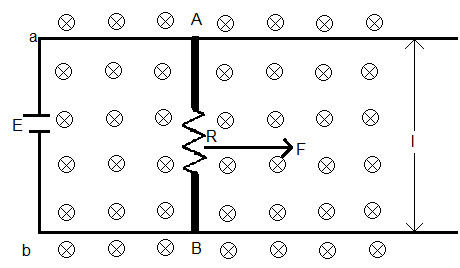
Now, due this force, the rod will accelerate towards right.
Due to this, the magnetic flux through the loop will increase.
Magnetic flux in this case will be given as $\phi =BA$, where A is the area of the loop.
Since the rod is moving towards the right, the area of the loop will increase.
Suppose the rod moves a distance of dx in time dt.
The change in area of the loop in dt time will be equal to ldx.
Hence, there will be a change in flux of $d\phi =Bldx$.
When the flux through a loop changes with respect to time, it induces an emf in the loop that opposes the flow of current in the circuit.
The magnitude of induced emf is given as ${{E}_{induced}}=\dfrac{d\phi }{dt}$.
Therefore, ${{E}_{induced}}=\dfrac{d\phi }{dt}=\dfrac{Bldx}{dt}$.
$\dfrac{dx}{dt}$ will be the speed of the rod.
Hence, ${{E}_{induced}}=Blv$.
Now, the net emf in the circuit will be $E-{{E}_{induced}}$.
Hence, the circuit current will reduce to $i=\dfrac{E-{{E}_{induced}}}{R}=\dfrac{E-Blv}{R}$.
Substitute this value of current in equation (ii).
$F=\dfrac{E-Blv}{R}lB$ …… (iii)
As the speed of the rod increases, the induced emf also increases and after some time, the net emf will become zero. Thus the force will become zero. From this point of time, the rod will move with a constant speed i.e. terminal speed.
 Equate F to zero in equation (iii).
$F=0=\dfrac{E-Blv}{R}lB$
$\Rightarrow E-Blv=0$
Therefore, $v=\dfrac{E}{Bl}$.

Note: Let us find the time at which the rod will attain the terminal velocity from the time when it just starts its motion.
For this use equation (iii).
$F=\dfrac{E-Blv}{R}lB$.
We know that F=ma and $a=\dfrac{dv}{dt}$.
Therefore, $m\dfrac{dv}{dt}=\dfrac{E-Blv}{R}lB$
$\Rightarrow m\dfrac{dv}{E-Blv}=\dfrac{lB}{R}dt$
Integrate both the sides.
$\Rightarrow m\int\limits_{0}^{v}{\dfrac{dv}{E-Blv}}=\dfrac{lB}{R}\int{dt}$
$\Rightarrow m\left. \ln \left( E-Blv \right) \right|_{0}^{v}=\dfrac{lB}{R}t$
$\Rightarrow m\ln \left( \dfrac{E-Blv}{E} \right)=\dfrac{lB}{R}t$.
$\Rightarrow t=m\dfrac{R}{lB}\ln \left( \dfrac{E-Blv}{E} \right)$
When the value of v is equal to terminal velocity, $E-Blv=0$.
$\Rightarrow \ln \left( \dfrac{E-Blv}{E} \right)=\ln 0=\infty $
Therefore, $t=\infty $.
This means that the rod will approach a terminal speed at infinite time. Therefore, in reality the rod will never approach the terminal velocity.