Question

AD is one of the median of a \[\Delta {\text{ABC}}\] . X is any point on AD. Show that \[{\text{arc(}}\Delta {\text{ABX)}} = {\text{arc(}}\Delta {\text{ACX)}}\] .

Answer 1

Hint: Here we are asked to prove \[{\text{arc(}}\Delta {\text{ABX)}} = {\text{arc(}}\Delta {\text{ACX)}}\] . First draw the triangle ABC with the given conditions. Observe the triangle carefully, recall the concepts of median and apply those concepts to find the relation between \[{\text{arc(}}\Delta {\text{ABX)}}\] and \[{\text{arc(}}\Delta {\text{ACX)}}\] .

Complete step-by-step answer:
Given a triangle ABC where AD is one of the median and X is any point on AD.
Let us first draw the triangle with the given conditions.

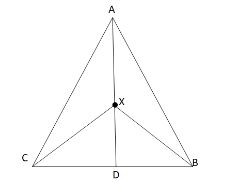
As AD is the median it divides the \[\Delta {\text{ABC}}\] into two equal two congruent triangles which are \[\Delta {\text{ACD}}\] and \[\Delta {\text{ABD}}\] .
Therefore we can say,
 \[{\text{arc(}}\Delta {\text{ABD)}} = {\text{arc(}}\Delta {\text{ACD)}}\] (i)
We observe that for \[\Delta {\text{CXB}}\] , XD is its median therefore, the triangles \[\Delta {\text{XCD}}\] and \[\Delta {\text{XBD}}\] are congruent triangles. So we can write,
 \[{\text{arc(}}\Delta {\text{XBD)}} = {\text{arc(}}\Delta {\text{XCD)}}\] (ii)
Now, we subtract equation (ii) from (i),
 \[{\text{arc(}}\Delta {\text{ABD)}} - {\text{arc(}}\Delta {\text{XBD)}} = {\text{arc(}}\Delta {\text{ACD)}} - {\text{arc(}}\Delta {\text{XCD)}}\] (iii)
From the figure we observe that subtracting \[{\text{arc(}}\Delta {\text{XBD)}}\] from \[{\text{arc(}}\Delta {\text{ABD)}}\] gives us \[{\text{arc(}}\Delta {\text{ABX)}}\] .
So we can write \[{\text{arc(}}\Delta {\text{ABD)}} - {\text{arc(}}\Delta {\text{XBD)}} = {\text{arc(}}\Delta{\text{ABX)}}\] (iv)
Also we observe that subtracting \[{\text{arc(}}\Delta {\text{XCD)}}\] from \[{\text{arc(}}\Delta{\text{ ACD)}}\] gives us \[{\text{arc(}}\ {\text{Delta ACX)}}\]
So we can write \[{\text{arc(}}\Delta {\text{ACD)}} - {\text{arc(}}\Delta {\text{XCD)}} = {\text{arc(}}\Delta{\text{ACX)}}\] (v)
Now, substituting equation (iv) and (v) in equation (iii) we get
 \[{\text{arc(}}\Delta {\text{ABX)}} = {\text{arc(}}\Delta{\text{ ACX)}}\]
Hence, we proved \[{\text{arc(}}\Delta {\text{ABX)}} = {\text{arc(}}\Delta{\text{ ACX)}}\] .

Note: Median of a triangle is a line that joins the one of the vertex of the triangle to its opposite side such that it divides the opposite side into two equal parts or we can say a median divides the triangle into two congruent triangles. If the medians are drawn from all three vertices of a triangle then all the three medians would intersect at a point, this point is known as centroid