Question

$AD$ and $GD$ are medians of $\vartriangle ABC\,\,and\,\vartriangle DEF$. If $\vartriangle ABC\sim \vartriangle DEF$. Then$\dfrac{AD}{DG}=\dfrac{BC}{EF}$
$\begin{align}
  & \left( A \right)\,True \\
 & \left( B \right)False \\
\end{align}$

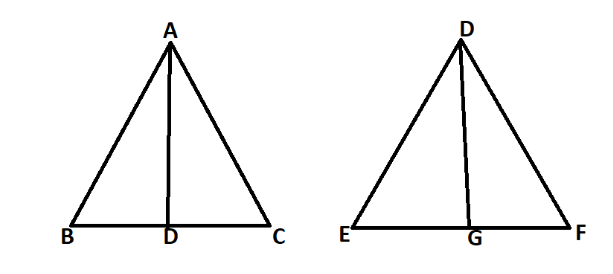
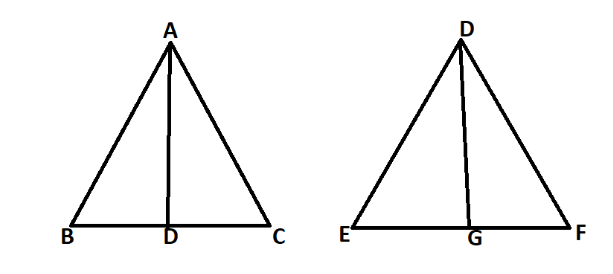
Answer 1

Hint: For this question, first apply Basic proportionality theorem to get the ratio of sides of the triangle after that rearrange it with the help of condition of similarity of triangles and at last conclude for true or false.

Complete step-by-step answer:
It is given in the question,
$\vartriangle ABC\sim \vartriangle DEF$
We know that, in similar triangles, corresponding angles are equal and corresponding sides are in the same ratio.
Therefore,
$\angle A=\angle D,\angle B=\angle E,\angle C=\angle F$
 and
$\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}$
We also know that medians divide the triangle in two equal parts, so that
$\dfrac{1}{2}\angle A=\dfrac{1}{2}\angle D$
From the figure,
$\therefore \angle BAD=\angle EDG$ ………………………….(I)
Now, we have to prove $\vartriangle BAD$ and $\vartriangle EDG$ are similar.
Therefore, we will apply similarity criteria.
In $\vartriangle BAD$ and $\vartriangle EDG$,
$\angle B=\angle E$ ………………………..(ii)
$\because $$\vartriangle ABC\sim \vartriangle DEF$
$\angle BAD=\angle EDG$ …………………..(iii)
Because, if the whole angle is equal then its halves are also equal.
We know that when two angles are equal then the triangle will similar by AA similarity criterion, so that
$\vartriangle BAD$$\sim $$\vartriangle EDG$
It means they also follow the condition of similar triangle, so that
$\dfrac{AB}{DE}=\dfrac{AD}{DG}=\dfrac{BD}{EG}$ ………………(iv)
Because of it is given in the question,
$\vartriangle ABC\sim \vartriangle DEF$
So that we can also write
$\dfrac{AB}{DE}=\dfrac{BC}{EF}$ …………………(v)
From equations (iv) and (v) we can say that
$\dfrac{AD}{DG}=\dfrac{BC}{EF}$

Hence, we can say that the above condition is true.

Note: Similar figures- When two geometrical figures are said to be similar , if they have the same shape but same size is not necessarily.
Congruence object- Two objects are said to be congruent, if they have the same size.