Question

AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters
(ii) ABCD is a rectangle

Answer 1

Hint: In the solution we will use the property of a quadrilateral. The property used in this problem is that opposite angles of the cyclic quadrilateral is supplementary.

Complete Step-by-step Solution
The circle through points A, B and C intersects CD at point E.
 The following is the schematic diagram of the parallelogram.

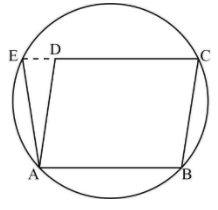
In the cyclic quadrilateral ABCE the sum of angle is,
$\angle AED + \angle ABC = 180^\circ $……(i)
  Also, we know that the opposite angles of a quadrilateral are supplementary.
$\angle ADE + \angle ADC = 180^\circ $
Since, from the linear pair axiom theorem which states that when a ray stand on the line then, addition of two adjacent angles will be equal to $180^\circ $. We know that the angle $\angle ADC$ is equal to $\angle ABC$.
On putting angle $\angle ABC$ for $\angle ADC$ in the above expression.
$\angle ADE + \angle ABC = 180^\circ $…….(ii)
On equating equations (i) and (ii).
$\begin{array}{c}
\angle AED + \angle ABC = \angle ADE + \angle ABC\\
\angle AED = \angle ADE
\end{array}$
Now, in the triangle $\Delta ADE$the sides AE and AD are equal because angle $\angle AED = \angle ADE$ are equal.
Therefore, it is proved that \[AE = AD\].

Note:In solving such types of problems, make sure to learn the property of a triangle and quadrilaterals. The one of the most important point is that while applying the linear pair axiom theorem, students should be careful about the sum of adjacent angles which is $180^\circ $ not $360^\circ $.