Question

Absorption of a gas follows Freundlich adsorption isotherm $x$ is the mass of the gas adsorbed on mass $m$ of the adsorbent. The plot of $\log \dfrac{x}{m}$ versus $\log p$ is shown in the given graph $\dfrac{x}{m}$ Is proportional to:

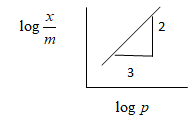
a.) ${{P}^{\dfrac{3}{2}}}$
b.) ${{P}^{3}}$
c.) ${{P}^{\dfrac{2}{3}}}$
d.) ${{P}^{2}}$

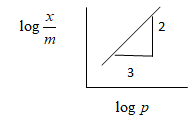
Answer 1

Hint: The relation between $\dfrac{x}{m}$ and $P$ can be shown as $\dfrac{x}{m} = K.{{P}^{\dfrac{1}{n}}}$ ,apply natural log on both sides of the above equation and try to find out the slope of the graph obtained by the equation obtained after applying the log on both sides to find the answer for the above question.

Complete step by step solution:
We are having the relation between $\dfrac{x}{m}$ and $P$ as $\dfrac{x}{m}=K.{{P}^{\dfrac{1}{n}}}$
Apply log on both sides, we obtain the following equation after applying the $\log $
$\log \dfrac{x}{m}=\log K+\dfrac{1}{n}\log P$

The graph of this equation is given as shown in the above diagram, where the slope of the graph of $\log \dfrac{x}{m}versus\log P$ is $\dfrac{1}{n}$ and the intercept is $\log K$
From the above given graph we obtained the slope as $\dfrac{1}{n}=\dfrac{2}{3}$
Put this slope in the above equation of the Freundlich adsorption isotherm
We obtain the final equation using the data given from the above graph is
$\dfrac{x}{m}=K.{{P}^{\dfrac{2}{3}}}$
This shows the relation between $\dfrac{x}{m}$ and $P$ as $\dfrac{x}{m}$ is directly proportional to ${{P}^{\dfrac{2}{3}}}$
So, the correct answer is “Option C”.

Note: From the relation $\dfrac{x}{m}=K.{{P}^{\dfrac{1}{n}}}$ it is a bit complicated to find the value of the power of $P$. We applied natural log on both sides so that we obtain a linear equation which represents the equation of a straight line. By plotting the graph of the equation we can simply calculate the slope which is nothing but the power of $P$ and further putting the value of the slope in the original relation we obtained the required answer. This is one of the easier methods of finding unknowns of this type.