Question

What is the abscissa of any point on $y - $ axis?

Answer 1

Hint: Here we have to use the concept of coordinates and graphs. We know the representation of coordinates on a graph is like $(x,y)$ where $x$ represent the abscissa and $y$ represent ordinate. Finally we conclude the answer by using the discussion of examples and get the required answer.

Complete step-by-step solution:
Now we assume a coordinate $A(x,y)$ where $x$ represents the abscissa and $y$ represent ordinate.
If point $A(x,y)$ moves left and right on a graph so the abscissa of coordinate $A$ becomes changed.
For example a coordinate $(2,3)$ moves right through $1$ unit distance so the coordinates becomes $(3,3)$.
If a coordinate $(2,3)$ moves left through $1$ unit distance so the coordinate $(1,3)$
If we can say that the point $A(x,y)$ moves upward and downloads on a graph then ordinate or coordinate $A$ becomes changed.
For example we can take a coordinate $(2,3)$ moves upward through $1$ unit distance so the coordinates become $(2,4)$.
If we take the coordinate $(2,3)$ moves downward through $1$ unit distance so the coordinates become $(2,2).$

Note: If a point on $y - $ axis is the representation of coordinates on $y - $ axis like $(0,y)$ and then if we move point right and left on a graph so the abscissa of coordinates does not change it’s always zero But if we move point upward and downward so the ordinate of coordinates becomes changed. So, the abscissa of any point on the $y - $ axis is always zero.

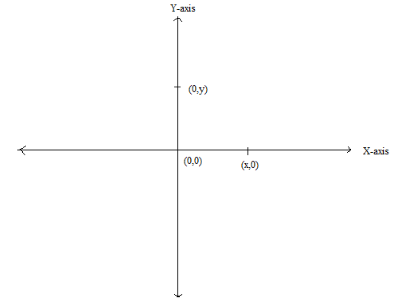
In such types of problems we have to assume a point on the graph and try to move the point on the graph in all four directions then observe the changes in point while moving in a specific direction. In case of any point on the $y$ axis so the abscissa of such types of coordinates is always zero.