Question

\[ABCD\] is quadrilateral in which \[AB\parallel CD\]. If \[AD = BC\], show that, \[\angle A = \angle B\] and \[\angle C = \angle D\].

Answer 1

Hint: At first, we consider a construction such that a parallel line \[CE\] from \[C\] which meets \[AB\] at \[E\].
By joining the B and E we get a line AE which is parallel to DC, hence here we have got two sets of parallel lines that are joined, which is one of the properties of parallelogram.
By using the properties of parallelogram we can construct a parallelogram and prove the theorem.
Properties of parallelogram are:
Two opposite sides of a parallelogram are parallel and equal to each other.
Sum of the supplementary angles of parallelogram \[{180^ \circ }\].

Complete step-by-step answer:

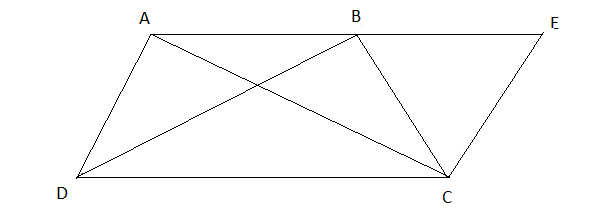
It is given that; \[ABCD\] is quadrilateral in which \[AB\parallel CD\].
We have to prove that, \[\angle A = \angle B\] and \[\angle C = \angle D\].
Let us draw a parallel line \[CE\] which is parallel to \[AD\] from \[C\]which meets \[AB\] at \[E\].
It is given that, \[AB\parallel CD\] and we can see that by construction of parallelogram \[AD\parallel CE\].
Therefore from our construction we can come to a conclusion that the points \[AECD\] forms a parallelogram.
Hence by using the property of a parallelogram we get,
\[AD = EC\]
It is also given that, \[AD = BC\]
So, we have found that \[EC = BC\]
Form \[\Delta BEC,EC = BC\], then we have,
\[\angle CBE = \angle CEB\]… (1)
We know that,
\[\angle ABC + \angle CBE = {180^ \circ }\]…. (2) As they are linear pairs.
That is they are joined together to form a straight line.
Again, \[AD\parallel CE\]and \[AE\]is the transversal.
Then we have,
\[\angle DAB + \angle CEB = {180^ \circ }\]… (3)
From (2) and (3) we have,
\[\angle ABC + \angle CBE = \angle DAB + \angle CEB\]
Since, \[\angle CBE = \angle CEB\]
On simplifying using the equation (1) we have, \[\angle A = \angle B\]
Since, \[AB\parallel CD\]
\[\angle A + \angle D = {180^ \circ }\]… (4)
And,
\[\angle B + \angle C = {180^ \circ }\]… (5)
From (4) and (5) we have,
\[\angle A + \angle D = \angle B + \angle C\]
We already know that, \[\angle A = \angle B\]
So, \[\angle C = \angle D\]

Here, we have proved that \[\angle A = \angle B\] and \[\angle C = \angle D\].

Note: The sum of the interior angle on the same side of a transversal of two parallel lines is \[{180^ \circ }\]. Sum of the supplementary angles of parallelogram \[{180^ \circ }\]. And also we know that the angle formed by a straight line is \[{180^ \circ }\].
While proving the above problem we have used a parallelogram which is constructed by drawing a line CE parallel to AD. We further use the relations of angels mentioned in the additional information to achieve at our final result.