Question

ABCD is a trapezium. AB is parallel to DC, BD is a diagonal and E is the midpoint of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is midpoint of BC.

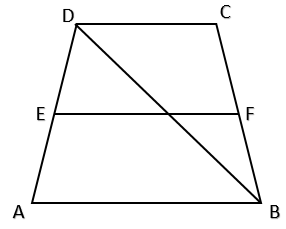
Answer 1

Hint: Now first consider the triangle ABD and use basic proportionality theorem. Now we know that E is the midpoint of AD hence ED = EA. Substituting this we get our first equation. Now consider the triangle BCD. Again use basic proportionality theorem and substitute the value obtained from equation (1). Hence we will arrive at the required result.

Complete step-by-step answer:
Now let us say the point of intersection of BD and EF is O.
Hence we have the figure as,

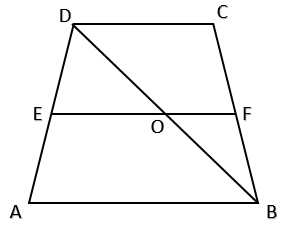
Now we know that ABCD is a trapezium.
Hence AB is parallel to CD.
Now we are given that through E a line is drawn Parallel to AB.
Hence we have EF is parallel to AB.
Now we can say that $DC\parallel EF\parallel AB$
Now consider triangle ABD.
In this triangle ED = EA ………………….. (1)
Also we have EO parallel to AB.
Hence using basic proportionality theorem we get,
\[\dfrac{ED}{EA}=\dfrac{DO}{OB}\]
But from equation (1) we have ED = EA.
Hence we get, \[\dfrac{EA}{EA}=\dfrac{DO}{OB}\]
Hence we can say that $\dfrac{DO}{OB}=1$
Cross multiplying we get, DO = OB ………………………… (2)
Hence O is the midpoint of DB.
Now consider the triangle BCD.
In this triangle we have OF parallel to CD.
Now by angle bisector theorem we can say that,
$\dfrac{OB}{OD}=\dfrac{FB}{FC}$
Now from equation (2) we have OB = OD.
Hence we can say that, $\dfrac{FB}{FC}=1$
Now cross multiplying we get, FB = FC.
Hence we get that F is the midpoint of BC.
Hence the result is proved.

Note: Now instead of using basic proportionality theorem we can directly use the result that if a line is drawn through the midpoint of one side parallel to the other side then it bisects the third side of the triangle. The result can be easily proved by basic proportionality theorems.