Question

ABCD is a square in the figure, find x.

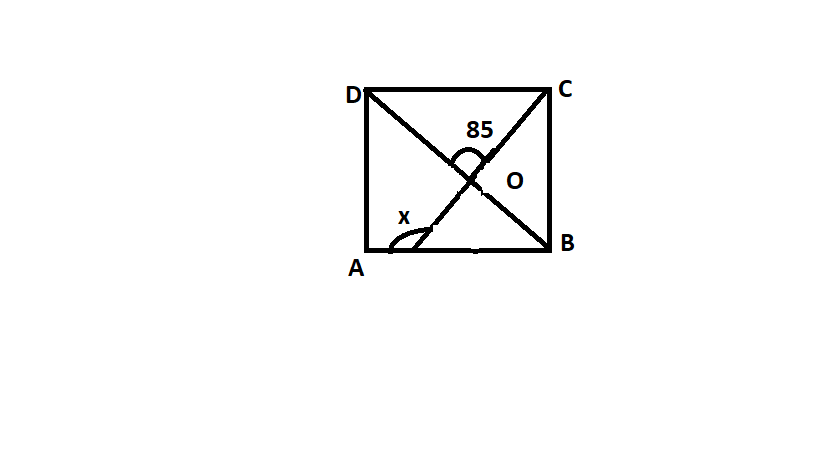
${\text{A}}{\text{. 15}}{0^ \circ }$
${\text{B}}{\text{. 13}}{0^ \circ }$
${\text{C}}{\text{. 12}}{0^ \circ }$
${\text{D}}{\text{.}}$ None of these

Answer 1

Hint: For a square, each angle is equal to 90 degrees, and the diagonals make an equal angle at every corner, use this to solve the question.

Complete step-by-step answer:

Given a square ABCD.
Using the figure shown below-

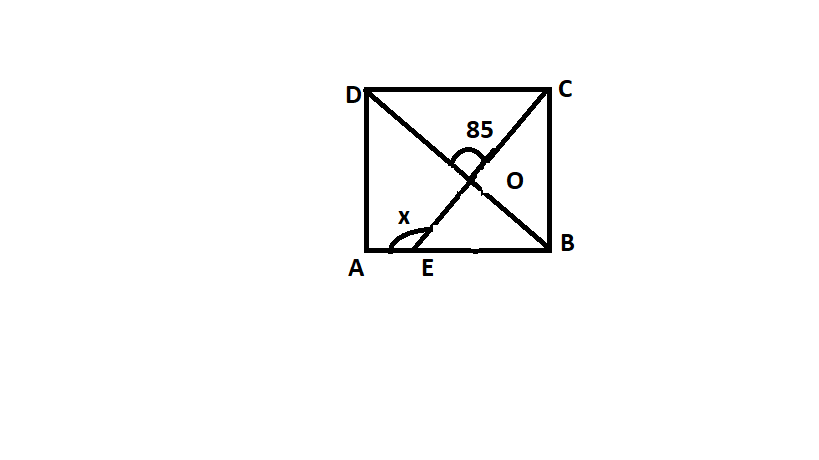
We have in triangle ABD,
AB = AD (sides of a square)
So, $\angle ADB = \angle ABD$
Now $\angle A = {90^ \circ }$ {angles of square are equal to 90 degrees}
Also, $\angle ADB = \angle ABD = \dfrac{{\angle A}}{2} = {45^ \circ }$
Now in triangle OEB
$\angle OEB + {85^ \circ } + {45^ \circ } = {180^ \circ }$ (By angle sum property)
$
  \angle OEB + {130^ \circ } = {180^ \circ } \\
  \therefore \angle OEB = {50^ \circ } \\
 $
Now, we can say, $x + \angle OEB = {180^ \circ }$ {Angles on a straight line}
$x = {180^ \circ } - \angle OEB = {130^ \circ }$.
Therefore, the value of x is 130 degrees.
Hence, the correct option is ${\text{B}}{\text{. 13}}{0^ \circ }$.

Note: Whenever such types of questions appear, then use the property of square to find the value of x. As mentioned in the question, all sides of square are equal, so AB = AD, so the angles $\angle ADB = \angle ABD = \dfrac{{\angle A}}{2} = {45^ \circ }$, then in triangle OEB, by using angle sum property find the value of angle OEB. And then find the value of x by using the concept of angles on a straight line.