Question

ABCD is a square, F is the midpoint of AB and E is the point on BC such that BE is one-third of BC. If area of $\Delta FBE=147{{m}^{2}}$, then the length of AC is,
(a) $21\sqrt{2}m$
(b) 63m
(c) $63\sqrt{2}m$
(d) $42\sqrt{2}m$

Answer 1

Hint: Assume the length of side of square line ‘a’ then change the values of FB and BE in terms of ‘a’, Then use the formula of triangle which is ½ x base x length where triangle is considered as FBE. Then use the diagonal formula, i.e., $\sqrt{2}(\text{side length})$ to find AC.

Complete step-by-step answer:
In the question we are given that ABCD is a square, F is a midpoint of AB. It is also said that BE is one third of BC.

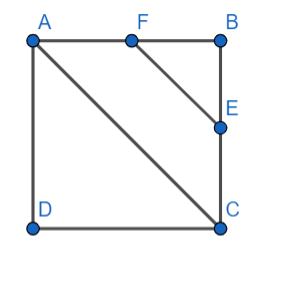
As it is given that ABCD is square so it takes its side length as ‘a’. Then as it was given F is a mid-point, so
$\begin{align}
  & AF=FB \\
 & \Rightarrow FB=\dfrac{1}{2}AB \\
\end{align}$
It is also given that BE is one third of BC, so
$BE=\dfrac{1}{3}BC$
As we know AB = BC = CD = DA = ‘a’, so we can take the side length of the square as ‘a’. Therefore, we can write it as,
$\Rightarrow FB=\dfrac{a}{2},BE=\dfrac{a}{3}$
Now we know, the area of the triangle is given by ½ times base and height.
Using this, let us consider triangle FBE, we can say that
$ar\left( \Delta FBE \right)=\dfrac{1}{2}\times FB\times BE$
Substituting the corresponding values, we get
$\begin{align}
  & ar\left( \Delta FBE \right)=\dfrac{1}{2}\times \dfrac{a}{2}\times \dfrac{a}{3} \\
 & \Rightarrow ar\left( \Delta FBE \right)=\dfrac{{{a}^{2}}}{12} \\
\end{align}$
In the question we are given that the area of triangle FBE is 147m2, so above equation can be written as,
$\begin{align}
  & \Rightarrow 147=\dfrac{{{a}^{2}}}{12} \\
 & \Rightarrow {{a}^{2}}=147\times 12=1764 \\
\end{align}$
Now taking square root on both sides, we get
a = 42
So the side of the square is 42m.
Now we know, AC is the diagonal of square which is of length $a\sqrt{2}$, then substituting the value of ‘a’, we get
$AC=42\sqrt{2}$
Hence, the correct option is (d).

Note: Students should be carrying out certain calculations and comparing and finding areas using formula ½ x base x height. They should also learn all the formulas by heart.
Another approach is considering right angled triangle ABC and using the Pythagoras theorem.

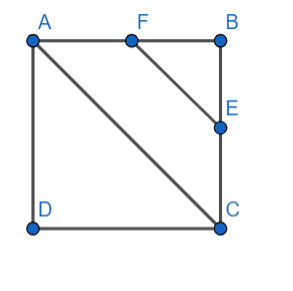
In this way also we will get the same answer but it will be a bit lengthy.