Question

ABCD is a square E, F, G, and H are points on AB, BC, CD, and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square. \[\]

Answer 1

Hint: We assume $\text{AE}=\text{BF}=\text{CG}=\text{DH}=x$ and use the equality of sides of square ABCD to deduce the sides of EFGH are equal, EF=FG=GH=HE. We take two right-angled triangles AEH and BEF and prove their congruence to deduce $\angle AEH+\angle BEF={{90}^{\circ }}$ from which we obtain $\angle HEF=\angle E={{90}^{\circ }}$. We extended the roof structure to another pair of congruent right triangles to prove all angles are right-angled, $\angle E=\angle F=\angle G=\angle H={{90}^{\circ }}$ \[\].

Complete step-by-step solution:

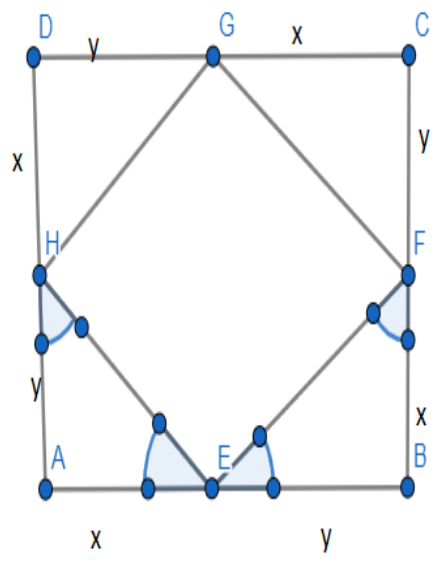
We have the required figure from the question where ABCD is a square and E, F, G and H are points on AB, BC, CD and DA respectively, such that
\[\text{AE}=\text{BF}=\text{CG}=\text{DH}\]
We know that lengths of all the sides of a square are equal. The sides in the above square are AB, BC, CD, and DA. So we have
\[AB=BC=CD=DA\]
We also know that all the interior angles of the square are right angles . So we have
\[\angle ABC=\angle BCD=\angle CDB=\angle DAB={{90}^{\circ }}\]
Let assume that $\text{AE}=\text{BF}=\text{CG}=\text{DH}=x$ and $AB=BC=CD=DA=a$ We use the equality of sides and have
\[\begin{align}
  & AB=AE+BE\Rightarrow a=x+BE \Rightarrow BE=a-x \\
 & BC=BF+CF\Rightarrow a=x+CF\Rightarrow CF=a-x \\
 & CD=CG+DG\Rightarrow a=x+DG\Rightarrow DG=a-x \\
 & DA=DH+AH\Rightarrow a=x+AF\Rightarrow BE=a-x \\
\end{align}\]
Let us assume$a-x=y$. We know from Pythagoras theorem that “In a right-angled triangle the square of the hypotenuse is the sum of squares of the other two sides.” So in right angled triangles AEH, BEF, CFG, and DGH we have the hypotenuses
\[HE=EF=FG=GH=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
 So we have found that the sides of the quadrilateral EFGH are equal. We only need to prove all the interior angles $\angle E,\angle F,\angle G,\angle H$of quadrilateral EFGH are right angles. Let us observe the triangles AEH and BEF. We have the sides AE=BF=$x$ , the right angles $\angle HAE=\angle EBF={{90}^{\circ }}$and the sides HA=EB=$y$. So by side-angle-side congruence of triangles we have
\[\Delta AEH\cong \Delta BEF\]
So by congruence we have equality between respective angles as
\[\angle AHE=\angle BEF,\angle AEH=\angle BFE\]
We know that the sum of the angles in a triangle is ${{180}^{\circ }}$. So we have,
\[\begin{align}
  & \angle AHE+\angle AEH+\angle EAH={{180}^{\circ }} \\
 & \Rightarrow \angle AEH+\angle AHE+{{90}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle AEH+\angle AHE={{90}^{\circ }}.....\left( 1 \right) \\
 & \angle BEF+\angle BFE+\angle EBF={{180}^{\circ }} \\
 & \Rightarrow \angle BEF+\angle BFE+{{90}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle BEF+\angle BFE={{90}^{\circ }}.....\left( 2 \right) \\
\end{align}\]
We add equation (1) and (2) and have,
\[\begin{align}
  & \angle AHE+\angle AEH+\angle BEF+\angle BFE={{180}^{\circ }}. \\
 & \Rightarrow \angle BEF+\angle AEH+\angle BEF+\angle AEH={{180}^{\circ }}\left( \because \angle AHE=\angle BEF,\angle AEH=\angle BFE \right) \\
 & \Rightarrow 2\left( \angle BEF+\angle AEH \right)={{180}^{\circ }} \\
 & \Rightarrow \angle BEF+\angle AEH={{90}^{\circ }} \\
\end{align}\]
We know that the sum of supplementary angles subtended on a straight line is ${{180}^{\circ }}$. So we have supplementary angles at the point E as
\[\begin{align}
  & \angle AEH+\angle HEF+\angle BEF={{180}^{\circ }} \\
 & \Rightarrow \angle HEF={{90}^{\circ }}\left( \because \angle BEF+\angle AEH={{90}^{\circ }} \right) \\
 & \Rightarrow \angle E={{90}^{\circ }} \\
\end{align}\]
We can similarly take pair of right angled triangles (EBF,FGC) , (FGC,GDH), (GDH,AEH) and use their congruence to prove to prove $\angle F=\angle G=\angle H={{90}^{\circ }}$. So in the quadrilateral EFGH we have
\[EF=FG=GH=HE,\angle E=\angle F=\angle G=\angle H={{90}^{\circ }}\]
Hence it is proved that EFGH is a square.

Note: If we would have only obtained $EF=FG=GH=HE$ then quadrilateral EFGH would have been a rhombus. IF we would have only obtained $\angle E=\angle F=\angle G=\angle H$ then quadrilateral EFGH would have been a rhombus rectangle. The length of the side of square EFGH is $\sqrt{{{a}^{2}}+{{\left( a-x \right)}^{2}}}$.