Question

ABCD is a rectangle such that $AC + AB = 5AD$ and $AC - AD = 8$, then the area of rectangle ABCD is _____________

Answer 1

- Hint: In this question we are going to calculate the area of the rectangle by using the definition of the rectangle that is opposite sides of the rectangle are equal and formula for finding the area of the rectangle. For calculating the sides of rectangle we use Pythagoras theorem, and the formula is written below
Formula Used:
The formula for finding the area of rectangle is =$length \times breadth$
And by using the definition of rectangle that is opposite sides of rectangle are equal,
Pythagoras theorem in a right angles triangle,
\[{\text{hypotenuse = }}\sqrt {{\text{perpendicular}}{{\text{r}}^{\text{2}}}{\text{ + bas}}{{\text{e}}^{\text{2}}}} \]


Complete step-by-step solution :

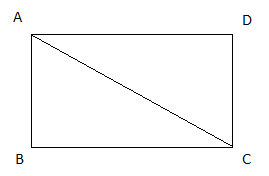
First we have to make a diagram of rectangle and name it ABCD
In the diagram, AB and DC and breadth and AD and BC are length of the
Rectangle
Now, According to definition of rectangle opposite sides are equal so we get,
AB=CD and AD=BC respectively ------------------ [1]
Now according to question
We have,
$AC + AB = 5AD$--------------- [2]
And $AC - AD = 8$---------------- [1]
Let AB=CD = \[y\]m
AD = BC = \[x\]m
And AC = \[z\]m
In triangle ABC, angle B is right angles triangle so we can apply Pythagoras theorem
\[{\text{hypotenuse = }}\sqrt {{\text{perpendicular}}{{\text{r}}^{\text{2}}}{\text{ + bas}}{{\text{e}}^{\text{2}}}} \]
Putting the values of hypotenuse, perpendicular and base in x, y, and z
We get,
$z = \sqrt {{x^2} + {y^2}} $ or \[{z^2} = ({y^2} + {x^2})\]----------------- [3]
Now from above equation [1] and equation [2]\[60squnits\]
$AC + AB = 5AD$
Writing above equation in x, y, and z
We get,
$z + x = 5y$
Subtracting both sides by x we get,
$z = 5y - x$
Now, squaring both sides to above equation we get,
${z^2} = {(5y - x)^2}$
Now we use the identity,
${(a - b)^2} = {a^2} + {b^2} - 2ab$
Now using this identity we open the above expression as, here a=5y and b=y we get,
${z^2} = (25{y^2} + {x^2} - 10xy)$-------------- [4]
Now, subtracting equation [3] from [4] we get,
\[{z^2} - {z^2} = (25{y^2} + {x^2} - 10xy - {y^2} - {x^2})\]
Now subtracting the like terms we get,
\[24{y^2} - 10xy = 0\]
Now taking y common from above equation we get,
\[y(24y - 10x) = 0\]
Since there will be two possibilities either y=0 or \[(24y - 10x) = 0\]
Since y cannot be equal to zero
So \[(24y - 10x) = 0\]
Solving above expression we get, by adding both sides by 10x
\[24y = 10x\]
Now dividing both sides by y we get,
\[24 = 10\dfrac{x}{y}\]
Dividing both sides by 10 we get,
\[\dfrac{x}{y} = \dfrac{{24}}{{10}}\]
Dividing numerator and denominator by 2 we get and by comparing numerator and denominator we get the values of x and y.
\[\dfrac{x}{y} = \dfrac{{12}}{5}\]
\[x = 12\] And \[y = 5\] ------------- [5]
Now using equation [1] we get,
$AC - AD = 8$
Expression above equation in x, y, and z we get
\[z - y = 8\]
Putting the value of y and adding both sides by y we get,
\[z = 8 + 5\]
Adding 8 and 5 we get,
Z= 13
Now we know that length of rectangle is AD=BC which is x m and breadth AB=CD which is y meters
We know that are of rectangle is, ${\text{length}}$$ \times$${{ breadth}}$
Putting the value of length and breadth we get,
Area of rectangle = \[x \times y\]
Putting the value of x and y from equation [5] we get,
Area of rectangle =\[12 \times 5\]
=\[60sq.units\]

Hence the area of rectangle ABCD is \[60sq.units\]

Note:
Use correct formulas for calculating the areas of the rectangle first, make diagrams and always use the property of the figure and make calculation simple and easy. By seeing the equation we have to analyze what is given by making a diagram first and make it understood and clear.