Question

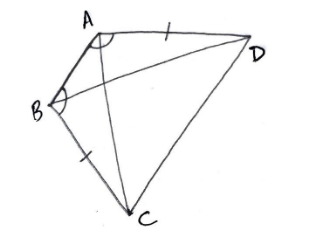
ABCD is a quadrilateral in which $ AD = BC $ and $ \angle DAB = \angle CBA $ . Prove that
(i) $ \Delta ABD \cong \Delta BAC $
(ii) $ BD = AC $
(iii) $ \angle ABD = \angle BAC $

Answer 1

Hint: 1. In a process of comparing two triangles if two sides and an angle of both of the triangles are equal then by the SAS (Side Angle Side) property, both of the triangles are congruent.
2. If two triangles are proved to be congruent then their angles and sides are also equal.

Complete step-by-step answer:
1. We are given the data that:
 $ AD = BC $
 $ \angle DAB = \angle CBA $
And, we have to prove:
 $ \Delta ABD \cong \Delta BAC $
2. Proof:
In $ \Delta ABD $ and $ \Delta BAC $
 $ AB = AB $ (Common side of both the triangles)
 $ \angle DAB = \angle CBA $ (Given that both angles are equal)
 $ AD = BC $ (Given that both the sides are equal)
3. Since in the above proof we have proved two sides and one angle of the triangle to be equal.
So, by SAS (Side Angle Side) property of congruence,
 $ \Delta ABD $ and $ \Delta BAC $ are proved to be congruent.
i.e. $ \Delta ABD \cong \Delta BAC $ .
4. Since, both the triangles $ \Delta ABD $ and $ \Delta BAC $ are proved congruent
Therefore, by using the property that two sides of congruent triangles can be equal. Sides $ BD = AC $ .
5. Now, both the triangles $ \Delta ABD $ and $ \Delta BAC $ are proved congruent
Therefore, by using the property that angles of congruent triangles are also equal
 $ \angle ABD = \angle BAC $

Note: If two triangles are proved to be congruent, then we can prove that any two sides or any two angles of the triangles are equal.