Question

ABCD is a quadrilateral in \[AB=CD\]and \[AD=BC\]. Show that it is a parallelogram.

Answer 1

Hint: In order to solve this question and show \[ABCD\] is a parallelogram, first do the construction and draw two diagonals \[AC\] & \[BD\] inside the figure \[ABCD\]. Then verify the SSS congruence rule between the triangles which states that in two triangles, if the three sides of one triangle are equal to the corresponding three sides (SSS) of the other triangle, then the two triangles are congruent. After that Use the property that opposite sides of a parallelogram are parallel to each other to show the given figure \[ABCD\] is a parallelogram.

Complete step-by-step solution:
According to the question, it is given that:
In figure \[ABCD\], \[AB=CD\]and \[AD=BC\]
We have to prove that \[ABCD\] is a parallelogram
In order to prove this question that is to show \[ABCD\] is a parallelogram, first do the construction and draw two diagonals AC & BD inside the figure \[ABCD\].

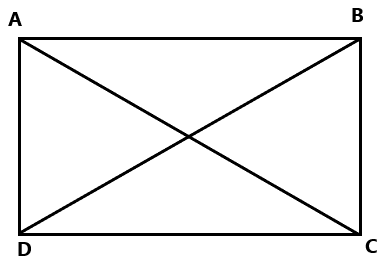
Proof: From the figure in \[\Delta \text{ABC}\]and \[\Delta \text{ADC}\]
\[AD=BC\] [Given in the question]
\[AB=CD\] [Given in the question]
\[AC=AC\] [Common side because it’s the diagonal]
∴ By SSS congruence rule which states that in two triangles, if the three sides of one triangle are equal to the corresponding three sides (SSS) of the other triangle, then the two triangles are congruent.
\[\therefore \Delta \text{ADC}\cong \Delta \text{ACB}\]
\[\Rightarrow \angle DAC=\angle ACB\]
\[\Rightarrow AB\parallel DC\] [Alternate interior angle property]
Now consider \[\Delta \text{ABD}\] and \[\Delta \text{DCB}\]
\[DB=DB\] [Common side because it’s the diagonal]
\[AD=BC\] [Given in the question]
\[AB=CD\] [Given in the question]
∴ By SSS congruence rule, \[\Delta \text{ABD}\cong \Delta \text{DCB}\]
\[\Rightarrow \angle ABD=\angle BDC\]
\[\Rightarrow AD\parallel BC\] [Alternate interior angle property]
Since \[AD\parallel BC\]and \[AB\parallel DC\].
According to the property we know that the opposite sides of a parallelogram are parallel to each other. Therefore, \[ABCD\] is a parallelogram.
Hence \[ABCD\] is a parallelogram.

Note: Some students prove this question by assuming that if opposite sides are equal implies, they are parallel also which is a completely wrong concept. It’s important to remember that in order to use such results one should check whether you can determine congruent pairs of triangles from it or not.