Question

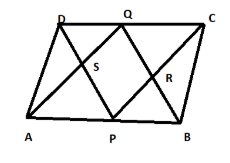
ABCD is a parallelogram in which “P” and “Q” are mid points of sides AB and CD respectively. If AQ intersects DP at S and BQ intersects CP at R, Show that
(a) APCQ is parallelogram
(b) DPBQ is parallelogram
(c) PSQR is parallelogram

Answer 1

Hint: Take properties of parallelogram and parallel lines transversal into consideration and get relation between angles and length of sides. Prove that the pairs of sides are parallel and equal to prove the quadrilateral to be parallelogram.

Complete step-by-step solution -
Given condition in the question is written as:
ABCD is a parallelogram P, Q are midpoints of AB, CD. In first part we need to prove that:
APCQ is a parallelogram
 

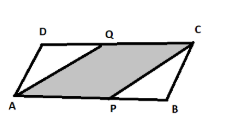
As we know AB is parallel to DC, we can say:
AP is parallel to QC.
As ABCD is given as a parallelogram, we can write equation:
AB=CD
By dividing with 2 on both sides of equation we get it as:
$\dfrac{AB}{2}=\dfrac{CD}{2}$
By substituting the mid points side length we get it as:
AP=QC
From above we get 2 equations of APCQ as:
AP=QC and AP parallel to QC.
So, opposite sides are parallel and opposite sides are of equal length.
It satisfies conditions of parallelograms:
So, APCQ is a parallelogram. Hence proved.
In the second part we need to prove the statement DPBQ is a parallelogram.

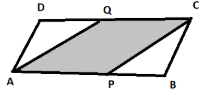
As ABCD is known to be a parallelogram, we get
AB is parallel to CD.
From above statement, we can say that
PB is parallel to QD.
As ABCD is a parallelogram, we can say that the sides: AB=CD
By dividing with 2 on both sides, we get the equation as:
$\dfrac{AB}{2}=\dfrac{CD}{2}$
By substituting mid points side lengths, we get PB=DQ
So, we proved opposite sides are parallel and equal.
So, DPBQ is a parallelogram. Hence proved.
In third part we need to prove that PQRS is a parallelogram
As we know that DPQB is a parallelogram DP is parallel to QB.

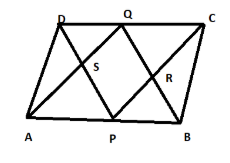
By the above statement, we can say that the lines: PS is parallel to QR.
As we also know APCQ is also a parallelogram; we can say:
AQ is parallel to PC
By above statements, we can say that the lines given by: SQ is parallel to PR
So, we get PS||QR, SQ||PR. So, pairs of opposite sides are parallel. From this we can say PQRS is a parallelogram.
Hence proved.

Note: Be careful while using parallelogram properties. Students generally confuse (as these many parallelograms are present) and unite adjacent sides are equal. But remember you cannot say anything about adjacent sides. After dividing with 2 write the mid points side which is present in the parallelogram, we all try to prove if you write the other side then it will be useless to this solution.