Question

ABCD is a field in the shape of a trapezium.
 $ AB||DC,\angle ABC={{90}^{\circ }},\angle DAB={{60}^{\circ }} $
Four sectors are formed with centres A, B, C, D. The radius of each sector is 17.5m. Find the total area of the four sectors.

Answer 1

Hint: Area of sector with angle $ \theta $ at the centre is given as $ \dfrac{{{r}^{2}}\theta }{2} $ , where $ \theta $ is present in radian. $ \pi $ radian has $ {{180}^{\circ }} $ angle. Angles formed by transversal on the same side of the parallel lines will have a sum of $ {{180}^{\circ }} $ . Use these concepts to get the area of four sectors.

Complete step-by-step answer:
We are given a quadrilateral with the condition as
 $ \begin{align}
  & AB||CD........................\left( i \right) \\
 & \angle ABC={{90}^{\circ }},\angle DAB={{60}^{\circ }}.........................\left( ii \right) \\
\end{align} $
So, we can draw a diagram with the help of above information as

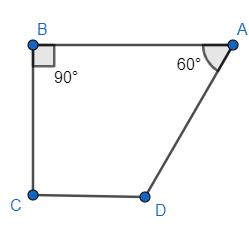
As we know angles formed by a transversal to two parallel lines has sum of $ {{180}^{\circ }} $ , if a line intersecting two parallel lines, then angles on the same side of transversal will have sum of $ {{180}^{\circ }} $ . So, $ AB||CD $ and BC is acting as transversal hence sum of angles
 $ \angle DCB,\angle ABC\to {{180}^{\circ }} $
So, we get
\[\begin{align}
  & \angle ABC+\angle DCB={{180}^{\circ }} \\
 & {{90}^{\circ }}+\angle DCB={{180}^{\circ }} \\
 & \angle DCB={{180}^{\circ }}-{{90}^{\circ }} \\
 & \angle DCB={{90}^{\circ }}..................................\left( iii \right) \\
\end{align}\]
Now, we know the sum of all interior angles in a quadrilateral is $ {{360}^{\circ }} $ . So, we get
 $ \begin{align}
  & \angle ABC+\angle DCB+\angle CDA+\angle DAB={{360}^{\circ }} \\
 & {{90}^{\circ }}+{{90}^{\circ }}+{{60}^{\circ }}+\angle CDA={{360}^{\circ }} \\
 & {{240}^{\circ }}+\angle CDA={{360}^{\circ }} \\
 & \angle CDA={{360}^{\circ }}-{{240}^{\circ }} \\
 & \angle CDA={{120}^{\circ }}.................................\left( iv \right) \\
\end{align} $
Hence, we can draw diagram as

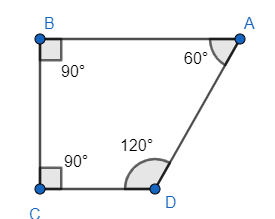
Now, we know the area of the circle is $ \pi {{r}^{2}} $ . The circle is a sector of angle $ 2\pi $ . So, we get
 $ \begin{align}
  & \text{Area by }2\pi \text{ angle of sector}=\pi {{r}^{2}} \\
 & \text{Area by }\theta \text{ angle of a sector}=\dfrac{\pi {{r}^{2}}}{2\pi }\times \theta \\
 & =\dfrac{{{r}^{2}}\theta }{2} \\
\end{align} $
Hence, we can get the area of all four sectors by adding areas of all the sectors by using $ \dfrac{{{r}^{2}}\theta }{2} $ here $ \theta $ is in radian. So,
Area of four sectors = Area of sector at A + Area of sector at B + Area of sector at C + Area of sector at D…………………..(v).
We know radius of each sector = 17.5m
 $ \begin{align}
  & \text{Area of sector at A}=\dfrac{{{r}^{2}}\theta }{2} \\
 & \theta =\dfrac{\pi }{3} \\
 & r=17.5m \\
 & \text{Area of sector at A}=\dfrac{{{\left( 17.5 \right)}^{2}}}{2}\times \dfrac{\pi }{3} \\
 & ={{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{6} \\
\end{align} $
\[\begin{align}
  & \text{Area of sector at B}=\dfrac{{{r}^{2}}\theta }{2} \\
 & \theta ={{90}^{\circ }}=\dfrac{\pi }{2},r=17.5m \\
 & \text{Area of sector at B}=\dfrac{{{\left( 17.5 \right)}^{2}}\times \pi }{2\times 2} \\
 & ={{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{2} \\
 & \text{Area of sector at C}=\dfrac{{{r}^{2}}\theta }{2} \\
 & r=17.5m \\
 & \theta ={{90}^{\circ }}=\dfrac{\pi }{2} \\
 & \text{Area of sector at C}=\dfrac{{{\left( 17.5 \right)}^{2}}}{2}\dfrac{\pi }{2} \\
 & ={{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{4} \\
 & \text{Area of sector at D}=\dfrac{{{r}^{2}}\theta }{2} \\
 & r=17.5m,\theta ={{120}^{\circ }}=\dfrac{2\pi }{3} \\
 & \text{Area of sector at D}=\dfrac{{{\left( 17.5 \right)}^{2}}}{2}\dfrac{2\pi }{3} \\
 & ={{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{3} \\
\end{align}\]
Now, we can get the area of four sectors by adding them. As we know the conversion of radian and degree can be done by the relation
 $ \begin{align}
  & {{180}^{\circ }}=\pi radian \\
 & {{1}^{\circ }}=\dfrac{\pi }{180}radian \\
\end{align} $
So, value of angles can be given in radians as
 $ \begin{align}
  & \angle A={{60}^{\circ }}=60\times \dfrac{\pi }{180}=\dfrac{\pi }{3} \\
 & \angle B={{90}^{\circ }}=90\times \dfrac{\pi }{180}=\dfrac{\pi }{2} \\
 & \angle C={{90}^{\circ }}=60\times \dfrac{\pi }{180}=\dfrac{\pi }{2} \\
 & \angle D={{120}^{\circ }}=120\times \dfrac{\pi }{180}=\dfrac{2\pi }{3} \\
\end{align} $
Area of four sector,
 $ \begin{align}
  & ={{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{6}+{{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{4}+{{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{4}+{{\left( 17.5 \right)}^{2}}\times \dfrac{\pi }{3} \\
 & {{\left( 17.5 \right)}^{2}}\left[ \dfrac{\pi }{6}+\dfrac{\pi }{4}+\dfrac{\pi }{4}+\dfrac{\pi }{3} \right] \\
 & {{\left( 17.5 \right)}^{2}}\left[ \dfrac{2\pi +6\pi +4\pi }{12} \right] \\
 & {{\left( 17.5 \right)}^{2}}\dfrac{12\pi }{12}={{\left( 17.5 \right)}^{2}}\times \pi \\
\end{align} $
Now, put the value of $ \pi \Rightarrow \dfrac{22}{7} $ . So, we get
Area of all four sectors
 $ \begin{align}
  & =17.5\times 17.5\times \dfrac{22}{7} \\
 & =962.5{{m}^{2}} \\
\end{align} $
Hence, the total number of four sectors is $ 962.5{{m}^{2}} $ .

Note: One may go wrong if he or she put value of $ \theta $ in the formula of area of sector i.e. $ \dfrac{{{r}^{2}}\theta }{2} $ , in degrees. Here, remember that $ \theta $ always will be in radian and so replace $ \pi \Rightarrow \dfrac{22}{7} $ at the end not by $ {{180}^{\circ }} $ . So, these kind of mistakes may happen with the students, so be clear with these concepts without using the property of parallel lines cutting by transversal (sum on same side of transversal $ {{180}^{\circ }} $ ) one may not be able to calculate $ \angle C $ . Don’t confuse it with the term sector; it is an arc in the circle. Angles given in the problem are the angles at the centre of their sector.