Question

$ABC$ is a triangle right-angled at $B$. And $D$ is a point on $BC$ produced $(BD > BC),$ such that $BD = 2DC.$ Which one of the following is correct?
(A) $A{C^2} = A{D^2} - 3C{D^2}$
(B) $A{C^2} = A{D^2} - 2C{D^2}$
(C) $A{C^2} = A{D^2} - 4C{D^2}$
(D) $A{C^2} = A{D^2} - 5C{D^2}$

Answer 1

Hint: All the options are in square terms. And the given triangle is a right angled triangle. So the best way to check for the correct answer is to use Pythagoras theorem. Find the relation between different sides using Pythagoras theorem and then use the given information in the question to check which option is correct.

Complete Step by Step Solution:
It is given in the question that,
$\Delta ABC$ is a right angle-triangle at $B$.
And $D$ is a point on $BC$ produced such that,
$BD = 2DC$.
By the help of the question we draw a figure as,

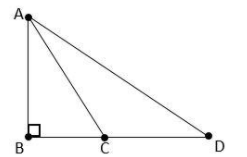
Here it is given that $BD = 2DC$ . . . . . . (1)
According to figure
$BC + CD = BD$
Put in equation (1)
Then,$BC + CD = 2DC$
$ \Rightarrow BC = 2CD - CD$
$ \Rightarrow BC = DC$
Now, in $\Delta ABC$
Hypotenuse$(H) = AC$
Base$(B) = BC$
Perpendicular$(P) = AB$
Therefore, by Pythagoras theorem. We can write,
${H^2} = {P^2} + {B^2}$
$ \Rightarrow A{C^2} = B{C^2} + A{B^2}$ . . . . . . (2)
Again, in $\Delta ABD$
Hypotenuse$(H) = AD$
Base$(B) = BD$
Perpendicular$(P) = AB$
Therefore, by using Pythagoras theorem. We can write,
${H^2} = {P^2} + {B^2}$
$ \Rightarrow A{D^2} = A{B^2} + B{D^2}$ . . . . . . (3)
Subtracting equation (3) from equation (2), we can write
$A{C^2} - A{D^2} = B{C^2} + A{B^2} - A{B^2} - B{D^2}$
$ \Rightarrow A{C^2} - A{D^2} = B{C^2} - B{D^2}$ . . . . . (4)
We know that $BD = 2DC$ and $BC = DC$
By substituting these values in equation (4), we get
$A{C^2} - A{D^2} = D{C^2} - {\left( {2DC} \right)^2}$
$ = D{C^2} - 4D{C^2}$
$ \Rightarrow A{C^2} - A{D^2} = - 3D{C^2}$
$ \Rightarrow A{C^2} = A{D^2} - 3D{C^2}$

Therefore, from the above explanation the correct answer is (A) $A{C^2} = A{D^2} - 3C{D^2}$

Note:
In such a type of question. First look at the options, think about what is given. Then decide which approach would be best and then start solving. Because, such questions can have more than one way of solving, but other ways might be lengthy or complex than the one that we used. The approach we used is the easiest approach for this question. You only need to know the Pythagoras theorem.