Question

ABC is a triangle in which $\angle $ B=$2$$\angle $C . D is a point on BC such that AD bisects $\angle $BAC and AB=CD . Prove that $\angle $ BAC= ${72^\circ }$ .

Answer 1

Hint: In this Question we have to draw one angle bisector at $\angle $ ABC which is joined at the point P on the line AC and Join P to D . Now observe carefully , Triangle APB congruence to Triangle DCP by SAS congruence criteria . Now perform some simple calculation we will find that the $\angle $ BAC= ${72^\circ }$ .

Complete step-by-step answer:
In this question it is given that $\angle $ B=$2$$\angle $C
Let us take $\angle $C = $y$ then $\angle $ B = $2y$ ;
It is also given that AD is the bisector of $\angle $BAC
So let us take $\angle BAD = \angle CAD = x$
Now Draw a line BP that is the angle bisector of $\angle ABC$ and Join PD as shown in the figure :

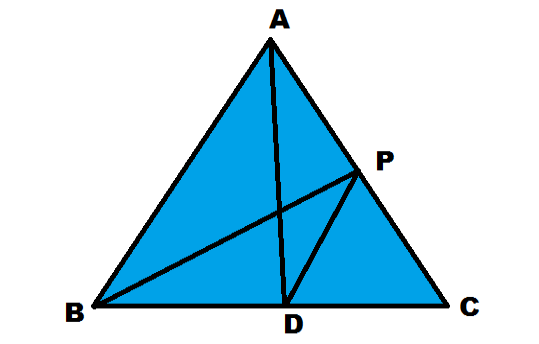
It is the required figure :
In triangle BPC,
$\angle $ CBP = $\angle $BCP = $y$ because BP is the angle bisector $\angle $ABC and is given that $\angle $ABC = $2y$
BP=PC because two adjacent angles are equal.
Now, In triangle ABP and triangle DCP,
$\angle $ ABP = $\angle $DCP = $y$
AB =DC already given
and BP=PC from above
So by SAS congruence criteria triangle ABP and triangle DCP are similar .
By the congruence of triangle
$\angle $ BAP = $\angle $ CDP and AP=DP
Therefore $\angle $ CDP= $2x$
$\angle $ ADP = $\angle $DAP = $x$ because AP=DP and $\angle $ A =$2x$ ,
In triangle ABD,
$\angle $ ADC = $\angle $ ABD + $\angle $ BAD
by putting the values that we are find above ,
$x + 2y = 2y + x$
$x = y$
In triangle ABC we have,
\[\angle A + \angle B + \angle C = {180^\circ }\] by the sum of interior angle of triangle ,
Now by putting the values of each
$2x + 2y + y = {180^\circ }$
As we prove that $x = y$
$5x = {180^\circ }$
$x = {36^\circ }$
Hence $\angle $BAC = $2x$ = ${72^\circ }$
Proved

Note: Always observe the question carefully and make a proper diagram then try to find out where you can apply the congruence criteria from the given condition . If any congruence criteria is not applied then try to make construction as we do in this question .
Always remember that if the two adjacent sides of a triangle are equal then the adjacent angle is also equal .
There are five ways to find out that two triangles are congruent: SSS, SAS, ASA, AAS and HL ( hypotenuse ,leg ).