Question

\[AB\] crystallizes in a body centred cubic lattice with edge length \['a'\]equal to \[387\,pm\]. The distance between oppositely charged ions in the lattice is:
(A) \[335\,pm\]
(B) \[250\,pm\]
(C) \[200\,pm\]
(D) \[300\,pm\]

Answer 1

Hint: As we know that the body centred cubic lattice is a unit cell in which number of atoms are present at eight corners as well as at the centre of the body. Distance between oppositely charged ions in the lattice can be calculated by calculating the radius of the atom.

Complete step by step answer:
As we know that the relation of edge length and radius of atom is calculated by face diagonal and body diagonal as shown below.
\[
d = 2r\\
r = \dfrac{{\sqrt 3 \,x\,a}}{4}
\]
Where \[a\]is the edge length of the body centred cubic lattice and \[r\]is the radius of the atom.
In this way, by putting the value of edge length we can calculate radius of atom as
\[
\Rightarrow r = \dfrac{{\sqrt 3 x387pm}}{4}\\
\Rightarrow r = \dfrac{{1.732x387pm}}{4}\\
\Rightarrow r = 167.57pm
\]
Now we know that the distance is the closest approach of two atoms so the relation between radius of atom and distance is as
\[d = 2r\]
Now we put the value of \[r\]to know the value of \[d\]
\[d = 2\,x\,167.57\,pm = 335.14\,pm\]

Note: The total number of atoms in a body centred cubic unit cell is 2 in which one from body centre and one from eight corners. The central atom in the body centred cubic lattice makes a body diagonal which can be calculated by face diagonal and the edge of the body centred cubic lattice by Pythagoras theorem. The body central atom also measures the distance of closest approach as we can see in the below diagram.

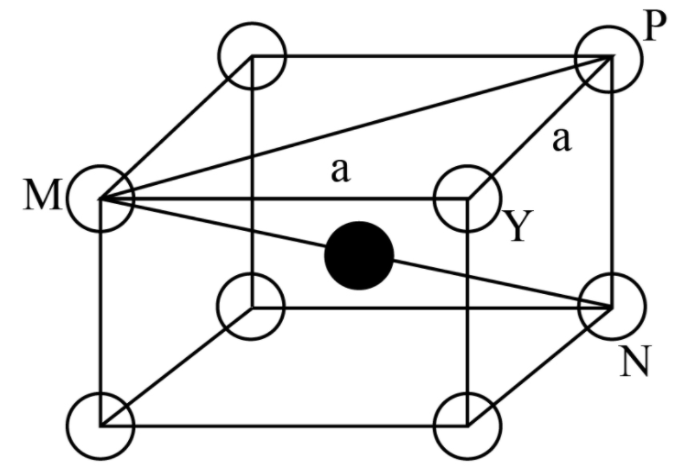
As the spheres at the body centre touches the spheres at the corners, body diagonal, \[{\rm{MN = 4r}}\]
Further, face diagonal,
\[
\Rightarrow {\rm{MP = }}\sqrt {{\rm{M}}{{\rm{Y}}^{\rm{2}}}{\rm{ + Y}}{{\rm{P}}^{\rm{2}}}} \,\,\\
\Rightarrow {\rm{ = }}\sqrt {{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{a}}^{\rm{2}}}} \\
\Rightarrow {\rm{ = }}\sqrt {\rm{2}} {\rm{a}}
\]
And body diagonal,
 \[
{\rm{MN = }}\sqrt {{\rm{M}}{{\rm{P}}^{\rm{2}}}{\rm{ + P}}{{\rm{N}}^{\rm{2}}}} \,\,\\
\Rightarrow {\rm{ = }}\sqrt {{\rm{2}}{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{a}}^{\rm{2}}}} \\
\Rightarrow {\rm{ = }}\sqrt {\rm{3}} {\rm{a}}
\]
Therefore, \[\sqrt {\rm{3}} {\rm{a = 4r}}\]
Or
\[r = \dfrac{{\sqrt 3 \,x\,a}}{4}\]