Question

When ${A_2}$ and ${B_2}$ are allowed to react, the equilibrium constant of the reaction at ${27^\circ }C$ is found $\left( {{K_c} = 4} \right)$.
${A_{2\left( g \right)}} + {B_2}_{\left( g \right)} \rightleftharpoons 2{\mathbf{A}}{{\mathbf{B}}_{\left( {\mathbf{g}} \right)}}$

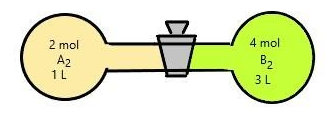
What will be the equilibrium concentration of \[{\mathbf{AB}}\]?
A) \[{\mathbf{1}}.{\mathbf{33M}}\]
B) \[{\mathbf{2}}.{\mathbf{66M}}\]
C) \[{\mathbf{0}}.{\mathbf{66M}}\]
D) \[{\mathbf{0}}.{\mathbf{33M}}\]

Answer 1

Hint: When the left flask is allowed to react with the right flask we can calculate their total volume, hence we can get their initial concentration to find the equilibrium concentration of \[AB\].

Complete step-by-step answer:
When the stop cork between two gases is removed, they are allowed to react. Then the reaction ${A_{2\left( g \right)}} + {B_2}_{\left( g \right)} \rightleftharpoons 2{\text{A}}{{\text{B}}_{\left( {\text{g}} \right)}}$ starts to happen. We are given the equilibrium constant, ${K_c} = 4$ and asked us to find the concentration of AB.

We know that equilibrium is a state of the process in which the concentration of reactants and products becomes constant until the conditions of temperature and pressure are unchanged. Now, we have to find the concentration of the two gases initially.
Therefore, when the stop cork is removed the gases are mixed. Hence the total volume becomes the sum of volumes of two of them
$Volume\;of\;container\; = \;1 + 3 = 4L$
Now, we can find the concentration.
Concentration is the number of moles per volume of the solution.
$Concentration\; = \dfrac{{\;number\;of\;moles}}{{volume}}$
Number of moles of $A$ is given as $2\;mol$ and $B$ is \[4{\text{ }}mol\].
Therefore,
$Concentration\;of\;A = \dfrac{2}{4} = 0.5\;mol/L$
And,
$Concentration\;of\;B = \dfrac{4}{4} = 1\;mol/L$

Now, let us consider equilibrium happens, at that time let us assume that some $x$ amount of A is reacted. Then in also, B $x$ amount is reacted since they are in the ratio of 1:1.

Now, on the reactant side, the concentration of A and B will be reduced by $x$. And the concentration of AB will be increased to $x$.
${A_2} + {B_2} \rightleftharpoons 2{\text{AB}}$

$0.5 - x$

$1 - x$

$2x$

So, we understand how the concentration is gained and reduced as the reaction happens. And at some point in time, this will reach equilibrium.
i.e.,
$Equilibrium\;Constant,\;{K_c} = 4$

And, $\;{K_c}$ is defined as the ratio of the product of the molar concentration of products to the product of the molar concentration of reactants, each raised to the power equal to its stoichiometric coefficient at a constant temperature.
$\Rightarrow {K_c} = \dfrac{{{{\left[ {AB} \right]}^2}}}{{\left[ {{A_2}} \right]\left[ {{B_2}} \right]}}$
$ \Rightarrow \;{K_c} = \dfrac{{{{\left( {2x} \right)}^2}}}{{\left( {0.5 - x} \right)\left( {1 - x} \right)}}$

Since the value of ${K_c}$ is given as 4
$4 = \dfrac{{4{x^2}}}{{\left( {0.5 - x} \right)\left( {1 - x} \right)}}$
On cross multiplying,
$\Rightarrow 4\left( {0.5 - x} \right)\left( {1 - x} \right) = 4{x^2}$
$\Rightarrow 0.5 - 0.5x - x + {x^2} = {x^2}$
After cancellation, we get
$\Rightarrow 1.5x = 0.5$
i.e., $\Rightarrow x = \dfrac{1}{3}$
The concentration of $AB$ is $2x$, Hence the concentration becomes $\dfrac{2}{3} = 0.66M$

Therefore, the correct answer is (C).

Note: In the case of a gaseous reaction, the equilibrium constant is calculated from partial pressures of gaseous reactant and products rather than their active masses and such an equilibrium is represented as ${K_p}$.