Question

A(1,0,0), B(0,2,0), C(0,0,3) from the triangle \[ABC\]. Then the direction ratios of the line joining orthocentre and circumference of \[\Delta ABC\] are
A. \[58,43,36\]
B. \[59, - 44, - 37\]
C. \[59, - 44, - 111\]
D. None of these

Answer 1

Hint: First of all, find the orthocentre and centroid of \[\Delta ABC\]. Then the direction ratios of the line joining orthocentre and circumcentre is equal to the direction ratios of the line joining orthocentre and centroid. So, use this concept to reach the solution of the given problem.

Complete step by step solution:
Let \[H\left( {a,b,c} \right)\] be the orthocentre of \[\Delta ABC\] as shown in the given below figure:

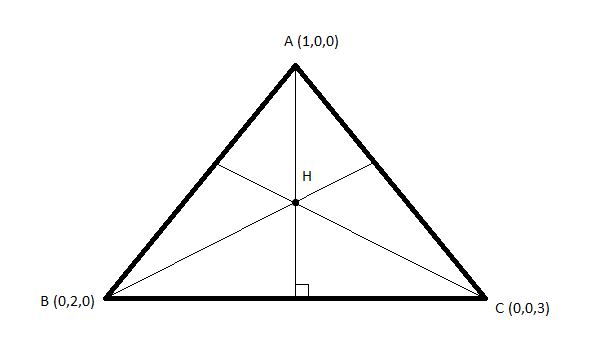
The direction ratios of the line joining \[AH\] are \[\left( {a - 1,b,c} \right)\] and the direction ratios of the line joining \[BC\] are \[\left( {0, - 2,3} \right)\].
We know that the condition of perpendicularity for two lines to be perpendicular to each other with direction ratios are \[\left( {{x_1},{y_1},{z_1}} \right)\] and \[\left( {{x_2},{y_2},{z_2}} \right)\]is given by \[{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2} = 0\]
Since, \[AH\] is perpendicular to \[BC\] we have
\[
   \Rightarrow \left( {a - 1} \right)\left( 0 \right) + \left( b \right)\left( { - 2} \right) + \left( c \right)\left( 3 \right) = 0 \\
   \Rightarrow - 2b + 3c = 0 \\
  \therefore b = \dfrac{3}{2}c \\
\]
The direction ratios of the line joining \[BH\] are \[\left( {a,b - 2,c} \right)\] and the direction ratios of the line joining \[CA\] are \[\left( {1,0, - 3} \right)\].
Since, \[BH\] is perpendicular to \[CA\] we have
\[
   \Rightarrow \left( a \right)\left( 1 \right) + \left( {b - 2} \right)\left( 0 \right) + \left( c \right)\left( { - 3} \right) = 0 \\
   \Rightarrow a - 3c = 0 \\
  \therefore a = 3c \\
\]
Clearly \[H\left( {a,b,c} \right)\] lies on the plane \[\dfrac{x}{1} + \dfrac{y}{2} + \dfrac{z}{3} = 1\]. So, we have
\[
   \Rightarrow \dfrac{a}{1} + \dfrac{b}{2} + \dfrac{c}{3} = 1 \\
   \Rightarrow \dfrac{{3c}}{1} + \dfrac{{\dfrac{3}{2}c}}{2} + \dfrac{c}{3} = 1{\text{ }}\left[ {\because a = 3c,b = \dfrac{3}{2}c} \right] \\
   \Rightarrow 3c + \dfrac{3}{4}c + \dfrac{c}{3} = 1 \\
   \Rightarrow \dfrac{{12 \times 3c + 3 \times 3c + 4 \times c}}{{12}} = 1 \\
   \Rightarrow 36c + 9c + 4c = 12 \\
   \Rightarrow 49c = 12 \\
  \therefore c = \dfrac{{12}}{{49}} \\
\]
By substituting \[c = \dfrac{{12}}{{49}}\] in \[a = 3c\], we have
\[
   \Rightarrow a = 3 \times \dfrac{{12}}{{49}} \\
  \therefore a = \dfrac{{36}}{{49}} \\
\]
By substituting \[c = \dfrac{{12}}{{49}}\] in \[b = \dfrac{3}{2}c\], we have
\[
   \Rightarrow b = \dfrac{3}{2} \times \dfrac{{12}}{{49}} \\
  \therefore b = \dfrac{{18}}{{49}} \\
\]
Hence, the orthocentre of the \[\Delta ABC\] is \[H\left( {a,b,c} \right) = \left( {\dfrac{{36}}{{49}},\dfrac{{18}}{{49}},\dfrac{{12}}{{49}}} \right)\].
We know that, the centroid of a triangle with sides \[\left( {{x_1},{y_1},{z_1}} \right),\left( {{x_2},{y_2},{z_2}} \right)\& \left( {{x_3},{y_3},{z_3}} \right)\] is given by \[\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\].
Hence, the centroid \[O\] of the triangle \[\Delta ABC\] with sides \[A\left( {1,0,0} \right),B\left( {0,2,0} \right),C\left( {0,0,3} \right)\] is given by
\[
   \Rightarrow O = \left( {\dfrac{{1 + 0 + 0}}{3},\dfrac{{0 + 2 + 0}}{3},\dfrac{{0 + 0 + 3}}{3}} \right) \\
  \therefore O = \left( {\dfrac{1}{3},\dfrac{2}{3},\dfrac{3}{3}} \right) \\
\]
We know that the direction ratios of the line joining orthocentre and circumcentre is equal to the direction ratios of the line joining orthocentre and centroid.
So, the direction ratios of the line joining orthocentre \[\left( {\dfrac{1}{3},\dfrac{2}{3},\dfrac{3}{3}} \right)\] and centroid \[\left( {\dfrac{{36}}{{49}},\dfrac{{18}}{{49}},\dfrac{{12}}{{49}}} \right)\] is given by \[\left( {\dfrac{{36}}{{49}} - \dfrac{1}{3},\dfrac{{18}}{{49}} - \dfrac{2}{3},\dfrac{{12}}{{49}} - \dfrac{3}{3}} \right) = \left( {\dfrac{{59}}{{147}},\dfrac{{ - 44}}{{147}},\dfrac{{ - 111}}{{147}}} \right)\]. Since, these are direction ratios we can cancel the common terms. Hence by cancelling 147 in all its denominators we have the centroid as \[\left( {59, - 44, - 111} \right)\] which is our required circumcentre.
Therefore, the direction ratios of the line joining orthocentre and circumcentre is \[\left( {59, - 44, - 111} \right)\]
Thus, the correct option is C. \[59, - 44, - 111\]

Note: The orthocentre of a triangle is the intersection of the triangle`s three altitudes. The circumcentre of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersects.