Question

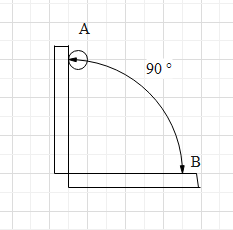
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is:

A. always radially outwards
B. always radially inwards
C. radially outwards initially and radially inwards later
D. radially inwards initially and radially outwards later

Answer 1

Hint: A bead is moving the wire bent in the form of quarter of a cycle. As the bead moves in the wire it moves as in a circular motion. So, we will also use the concept of circular motion and the centripetal force. From the free body diagram equate the forces to find the direction of the forces.

Complete step by step answer:
We have a wire bent in the form of a quarter of a circle. The bent wire is fixed vertically on ground. A bead is sliding down the bent wire. We need to find the direction of force on the moving bed in the wire.
Now, the bead is moving in the wire due to the gravitational force acting on the bead. Let the normal force acting on the bead is N. the normal force acting on the bead will be equal to the weight of the bead when the bead is at point A. as the bead slides along the wire, the normal force on the bead will be equal to the radial component of the weight towards the centre of the circle of which the wire is a part of.
 

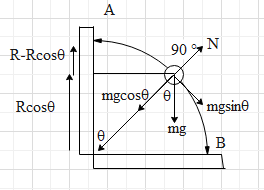
From the free body diagram of the system we can write that,
$N-mg\cos \theta =\dfrac{m{{v}^{2}}}{R}$
Where, $\dfrac{m{{v}^{2}}}{R}$ is the centripetal force acting on the body due to its motion on the bent wire which is a part of a circle.
Here. M is the mass of the bead, N is the normal force on the bead, g is the acceleration due to gravity, v is the velocity of the bead in the wire and R is the radius of the circle of which the bent wire is a part of.
From energy conservation we can say that, the loss in potential energy of the bead is equal to the kinetic energy gained by the bead.
So, we can write that,
$\begin{align}
  & mgR-mgR\cos \theta =\dfrac{1}{2}m{{v}^{2}} \\
 & g\left( R-R\cos \theta \right)=\dfrac{1}{2}{{v}^{2}} \\
 & v=\sqrt{2g\left( R-R\cos \theta \right)} \\
\end{align}$
Putting this value of the above equation we get that,
$\begin{align}
  & N-mg\cos \theta =\dfrac{m{{\left( \sqrt{2gR\left( 1-\cos \theta \right)} \right)}^{2}}}{R} \\
 & N-mg\cos \theta =\dfrac{m2gR\left( 1-\cos \theta \right)}{R} \\
 & N-mg\cos \theta =2mg-2mg\cos \theta \\
 & N=mg\left( 2-3\cos \theta \right) \\
\end{align}$
So, the force on the bead will be, $N=mg\left( 2-3\cos \theta \right)$
When $\theta ={{0}^{0}}$ , N is negative. So, it will be in the radially inward direction.
When $\theta $ increases, the value of N becomes less negative and when the value of $\theta $ is large, the value of N is positive. So, it will be in the radially outward direction.
So, the direction of force on the bead is radially inwards initially and radially outwards later.
The correct option is (D).

Note:
When the bead is in the position A, we have only the radial component of the force i.e. the radial component is maximum. The other component will be zero. As the bead moves the other component increases and the radial component decreases. So, we can directly say that the force is radially inward initially but with increase in the angle with the vertical it will be radially outward.