Question

A wire of length l is bent in the form of an equilateral triangle and carries an electric current $i$. Find the magnetic field B at centre.

Answer 1

Hint: We can use Biot-Savart Law to find the magnetic field at the centre of the triangle by each of its sides and sum up to obtain a net magnetic field.
Biot-Savart law describes the magnetic field at a point due to a small current carrying segment. This segment is considered as vector quantity and its direction is along the direction of current.

Formula used:
Magnetic field produced at a point due to a small current element, $\left| d\mathbf{B} \right|=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{Id\mathbf{l}\sin \theta }{{{r}^{2}}}$

Complete step-by-step answer:
Biot-Savart Law can be used to determine the magnetic field produced due to a small current element, $d\mathbf{l}$. Current element is a vector quantity and its direction is along the direction of current.
Biot-Savart Law states that magnetic field due to a current element is directly proportional to its length, current flowing through it and sine of angle between position vector and current element; and inversely proportional to square of distance of the point from the current element. Mathematically,
$\left| d\mathbf{B} \right|\propto \dfrac{Id\mathbf{l}\sin \theta }{{{r}^{2}}}$
$\Rightarrow \left| d\mathbf{B} \right|=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{Id\mathbf{l}\sin \theta }{{{r}^{2}}}$
The direction of the magnetic field is given by the right hand thumb rule which states that when we point the thumb of our right hand in the direction of the current element, the curved fingers show the direction of the magnetic field.
The figure below shows the equilateral triangle formed by the wire.

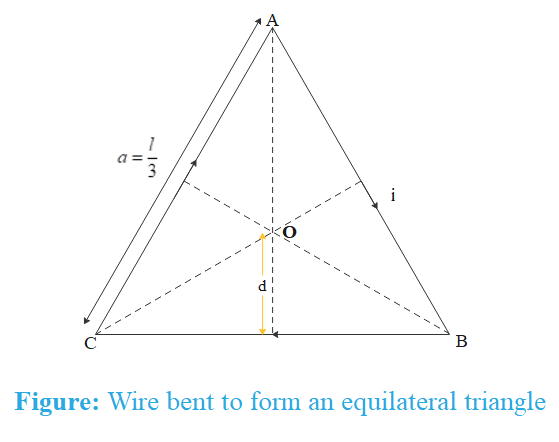
We have assumed that current flows clockwise. The magnetic field, as determined by right hand thumb rule, due to each side of the triangle is normally inward the plane of paper and hence can be summed up directly. Magnetic field due to each side of triangle is same due to symmetry and is given as
$\mathbf{B}=\dfrac{{{\mu }_{0}}i}{4\pi }\dfrac{\left[ \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right]}{d}$
Where d is the perpendicular distance of centroid from the wire.

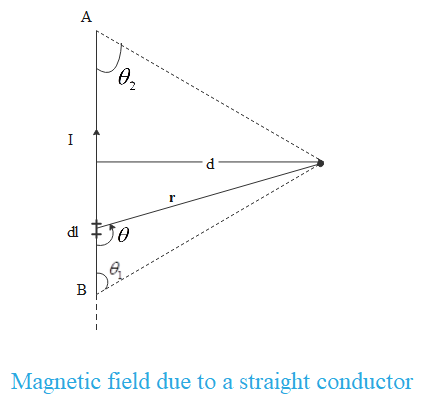
Substituting the values we get,
$\mathbf{B}=\dfrac{{{\mu }_{0}}i}{4\pi }\dfrac{\left[ \sin {{60}^{{}^\circ }}+\sin {{60}^{{}^\circ }} \right]}{(\dfrac{l}{6}\tan {{30}^{{}^\circ }})}=\dfrac{{{\mu }_{0}}i}{4\pi }\dfrac{18}{l}=\dfrac{9{{\mu }_{0}}i}{2\pi l}$
Total magnetic field due to triangle
$\mathbf{B}'=3B=\dfrac{27}{2}\dfrac{{{\mu }_{0}}i}{\pi l}$

Note: Magnetic field due to a straight infinite conductor is $\mathbf{B}=\dfrac{{{\mu }_{0}}I}{2\pi d}$
Biot-Savart Law can be used to determine the magnetic field produced due to a small current element, $d\mathbf{l}$. Current element is a vector quantity and its direction is along the direction of current.