Question

A wire of $3$ ohm resistance and $10cm$ length is stretched to $30cm$ length. Let us assume that it has a uniform cross section, what can be its new resistance?
$\begin{align}
  & A.27\Omega \\
 & B.9\Omega \\
 & C.3\Omega \\
 & D.30\Omega \\
\end{align}$

Answer 1

Hint: When a wire is stretched into a particular length, both its length as well as the area of cross-section will get changed. Even though its volume will always be constant. The area is given by the volume divided by the length of the wire. Substitute this in the equation of resistance and then find out the relation between the resistance of a wire and the length of the wire. Using this, find the new resistance. These all may help you to solve this question.

Complete step by step answer:
First of all let us mention what all are given in the question. The resistance of the wire originally is given as,

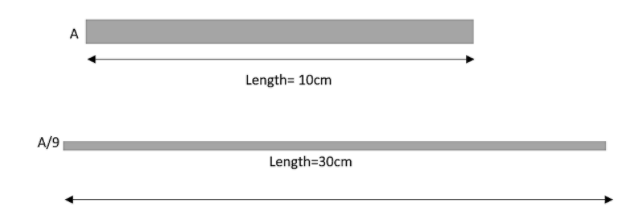
${{R}_{1}}=3\Omega $
Length of the wire at this condition is given as,
${{l}_{1}}=10cm$
In the second condition, the length has been changed where the new length is given as,
${{l}_{2}}=30cm$
This can be written in terms of original length as,
\[{{l}_{2}}=3{{l}_{1}}\]
Even though the length and area of the wire changes, the volume of the wire will remain constant.
The area can be expressed in terms of volume as,
\[A=\dfrac{V}{l}\]
Where \[V\] be the volume of the wire.
The resistance of a wire can be found using the equation,
\[R=\dfrac{\rho l}{A}\]
Where \[\rho \]be the resistivity of material.
Substituting the equation of area in this equation in will give,
\[R=\dfrac{\rho {{l}^{2}}}{V}\]
From this relation as the volume and resistivity are constant, we can see that,
\[R\propto {{l}^{2}}\]
Therefore we can write that,
\[\dfrac{{{R}_{1}}}{{{R}_{2}}}={{\left( \dfrac{{{l}_{1}}}{{{l}_{2}}} \right)}^{2}}\]
As we already mentioned,
\[{{l}_{2}}=3{{l}_{1}}\]
Substituting this in the equation will give,
\[\dfrac{{{R}_{1}}}{{{R}_{2}}}={{\left( \dfrac{{{l}_{1}}}{3{{l}_{1}}} \right)}^{2}}=\dfrac{1}{9}\]
From this we can see that the resistance of the wire increased \[9\]times than the original one. Therefore the final resistance will be,
\[{{R}_{2}}=9{{R}_{1}}=9\times 3=27\Omega \]
Therefore the correct answer is option A.

Note:
The resistance of a wire is a constant for a given area of cross section and length of wire. If the length of wire is increased, then the resistance also gets increased. If the area of the cross section is increased, the resistance will decrease.