Question

A wire $40\;cm$ long is bent into a rectangular frame $15\;cm \times 5\;cm$ and placed perpendicular to a field of induction $0.8\;T$ in $0.5\;s$. The frame is changed into a square frame and the field is increased to $1.4\;T$. Then the emf induced in the frame is:
A.$1.6\times 10^{-2}\;V$
B.$1.6\times 10^{3}\;V$
C.$1.6\times 10^{-4}\;V$
D.$1.6\times 10^{-5}\;V$

Answer 1

Hint: Begin by calculating the flux linked with the frame in both cases in terms of the applied magnetic field and the cross-sectional area bounded by the frame. Notice that the magnetic field and the area vectors are parallel to each other. Then, calculate the change in flux between both the cases. To this end, find the induced emf by defining it as the rate of change of magnetic flux linked with the frame, and you should arrive at the appropriate answer.

Formula Used:
Induced emf $\epsilon = -\dfrac{\Delta \phi}{\Delta t}$
Magnetic flux through the frame $\phi = \vec{B}.\vec{A} = BAcos\theta$.

Complete answer:
Let us approach this problem in the perspective of Faraday’s Laws of Electromagnetic Induction.
Faraday’s first law suggests that whenever the magnetic flux linked with a conductor changes, an emf is induced in the conductor. The induced emf exists as long as the change in magnetic flux continues to exist. Recall that magnetic flux here is nothing but the magnetic field lines.
In the scenario presented to us, the change in the magnetic flux is brought about by changing the cross-sectional area encompassed by the conducting wire and by changing the magnetic field strength after 0.5 seconds.
Using Faraday’s first law we can say that this change in flux introduces an emf or a potential difference across the ends of the conductor. This potential difference will induce a current that flows around the conductor.
Now, Faraday’s second law of electromagnetic induction states that the magnitude of induced emf in a conductor is equivalent to the rate of change of flux linked with the conductor. This is quantised as:
$\epsilon = -\dfrac{\Delta \phi}{\Delta t}$, where $\epsilon$ is the emf induced, $\phi$ is the magnetic flux. Note that the negative sign indicates that the direction of induced emf and the change in the direction of magnetic fields have opposite signs.
Now, we know that the magnetic flux through the conductor is given as $\phi = \vec{B}.\vec{A} = BAcos\theta$.
Since the conductor is placed perpendicular to the magnetic field B in both cases, the area vector A subtended by the frame is parallel to the magnetic field B $\Rightarrow \theta =0^{\circ} \Rightarrow cos\theta = cos 0^{\circ} = 1$
Therefore, $\phi = BA$
Now let us find the flux linked with both the frames.

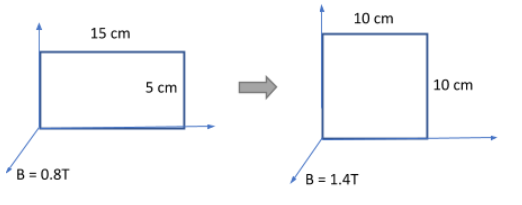
Initially, we have:
$B_1 = 0.8T$, $A_1 = 15 \times 5 \times 10^{-4} = 75 \times 10^{-4}\;m^2$. Therefore,
$\phi_1 = B_1 A_1 = 0.8 \times (75 \times 10^{-4}) = 60\times 10^{-4}\;Wb$
In the second case, we have:
$B_2 = 1.4T$, $A_2 = 10 \times 10 \times 10^{-4} = 10^{-2}\;m^2$. Therefore,
$\phi_2 = B_2 A_2 = 1.4 \times 10^{-2} = 140\times 10^{-4}\;Wb$
Therefore, the change in flux linked with the two frames is given as:
$\Delta \phi = \phi_2 - \phi_1 = (140-60) \times 10^{-4} = 80\times 10^{-4}\;Wb$
Thus, the rate of change of flux over time $t =0.5\;s$, which is nothing but the induced emf, is given as:
$\epsilon = -\dfrac{\Delta \phi}{\Delta t} = \dfrac{80 \times 10^{-4}}{0.5} = 160 \times 10^{-4} = 1.6 \times 10^{-2}\;V$

Therefore, the correct choice is A. $1.6 \times 10^{-2}\;V$

Note:
Recall that the other ways to change the emf induced in a coil in addition to changing the strength of the applied magnetic field and changing the area of cross-section bounded by the frame, i.e.,:
1. By establishing relative motion between the applied field and the frame.
2. By changing the number of turns of the frame.
3. By reversing the direction of the applied field.