Question

(a) Which physical quantity has its S.I. unit (1) Cm (Coulomb metre) and (2) N/C.
(b) Two point charges q and –q is placed at a distance ‘2a’ apart. Calculate the electric field at a point situated at a distance ‘r’ along the perpendicular bisector of the line joining the charges. What is the electric field when r>>a? Also, give the direction of the electric field w.r.t electric dipole moment?

Answer 1

Hint: The S.I. unit plays a very important role in determining the value of a physics quantity. Sometimes they are unique for different physical quantities and sometimes could be the same as well. Also, electric dipole is a setup of two charges in which two charges of equal magnitude are placed at a very small distance from each other.

Formula used:
$E = \dfrac{Kq}{d^2};\ K=\dfrac{1}{4\pi \epsilon_{\circ}}$

Complete step by step answer:
By observing the S.I. units, we can say that
(1) Cm is the product of charge and distance. Hence its S.I. unit of dipole moment.
(2) $\dfrac NC$ is the ratio of S.I. units of Force (N, newton) and charge (C, coulomb). Hence it is the force per unit charge which is the definition of Electric field. Hence it’s the S.I. units of electric field.
Now, we will find the expression for the electric field at the equatorial position of a dipole.

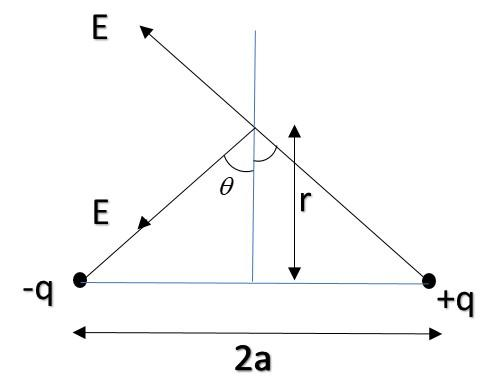
By symmetry, we can say that the field will only be in –x direction and not in y direction.
Now, electric field due to both charges can be resolved as $E_{net}$ as shown in the figure below:

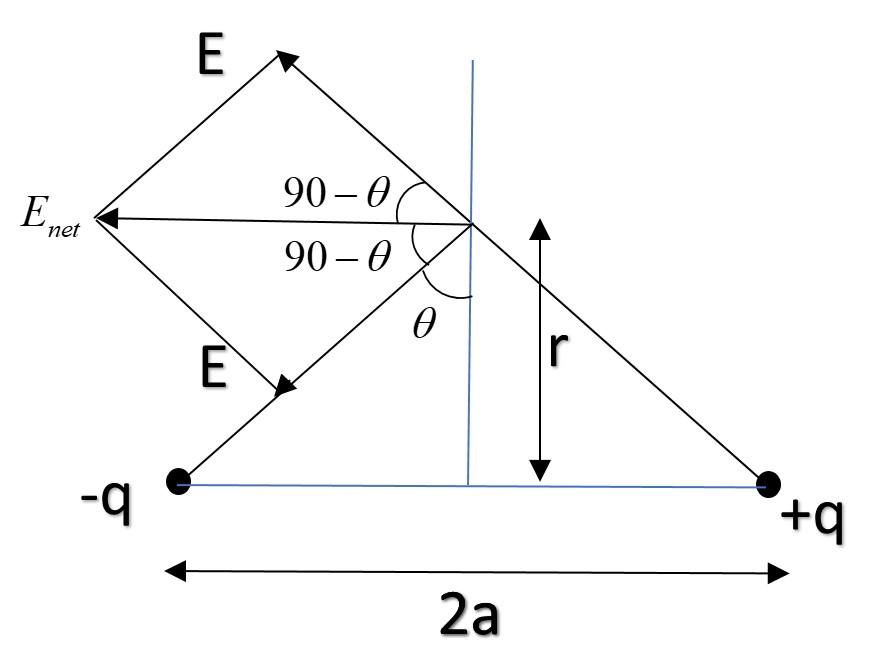
Now, $E = \dfrac{Kq}{d^2}$where $d^2 = r^2 + a^2$ [Using Pythagoras theorem]
Hence, $E = \dfrac{Kq}{r^2+a^2}$
Also, $E_{net} = E cos(90 - \theta) + Ecos(90 - \theta) = 2Esin\theta$
Now, in the figure,$sin\theta = \dfrac a{\sqrt{a^2+r^2}}$
Hence putting $E_{net} = 2\times \dfrac{Kq}{r^2+a^2} \times \dfrac a{\sqrt{a^2+r^2}} = \dfrac{2Kqa}{(r^2+a^2)^{3/2}}$
Now, if r>>a, $r^2+a^2 \approx r^2 and (r^2+a^2)^{3/2} \approx (r^2)^{3/2} = r^3$
Thus, $E_{net} = \dfrac{2Kqa}{r^3}$
Now, we know that dipole moment $\vec P$is the product of charge and distance between them, i.e. $P =q(2a)$
Hence $\vec E_{net} = \dfrac{K(2qa)}{r^3} = \dfrac{K\vec P}{r^3} = \dfrac{1}{4\pi\epsilon_{\circ}} \dfrac{\vec P}{r^3}$, hence its direction is in the direction of dipole moment (from +q to -q), which is perpendicular to the bisector.

Note:
Students should note that in the definition of dipole moment, we use to take the distance of charge from the centre of dipole. And in the formula, we take charge of any one and distance between them. Dipole moment is defined for charges of the same magnitude. It is a vector quantity with direction from +q to –q.