Question

A water tank is filled with water up to a height 8 m. A hole is made in the tank wall at a depth 3 m from the surface of water. Then the time taken to reach the ground
A. 1 sec
B. 2 sec
C. 3 sec
D. 4 sec

Answer 1

Hint: We can get the height of the hole from the ground by taking the difference of the two heights. As the water comes out of the hole, the time taken by it to reach the ground can be calculated by using the equations of motion. The initial velocity of the water before starting to fall is zero.
Formula used:
The equations of motion are given as
$
  v = u + at \\
  S = ut + \dfrac{1}{2}a{t^2} \\
  {v^2} - {u^2} = 2aS \\
$

Complete answer:

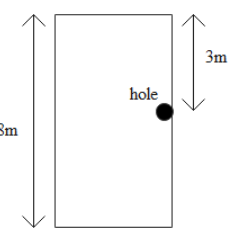
We are given a water tank which is filled with water up to a height 8 m. A hole is made in the tank wall at a depth 3 m from the surface of water. The height of this hole from the ground is given as $H = 8 - 3 = 5m$. The diagram shows the water tank with a hole punched in it.
Now we can use one of the equations of motion in order to find out the time taken by water to reach ground. We have the following equation that we can use to find out time.
$H = ut + \dfrac{1}{2}g{t^2}$
Here u is the initial velocity of the water before falling down and its value is obviously equal to zero. We can take $g = 10m/{s^2}$.
Now inserting the known values in the above equation, we get
$
  5 = 0 + \dfrac{1}{2} \times 10 \times {t^2} \\
   \Rightarrow {t^2} = 1 \\
   \Rightarrow t = 1s \\
$
Therefore, it takes 1 second for the water to reach the ground.

Hence, the correct answer is option A.

Note:
It should be noted that the water also possesses potential energy due to its position and height from the ground. Greater the height from the ground, higher is the potential energy. When a hole is punched in the tank, then water falls because the potential energy gets converted into kinetic energy.