Question

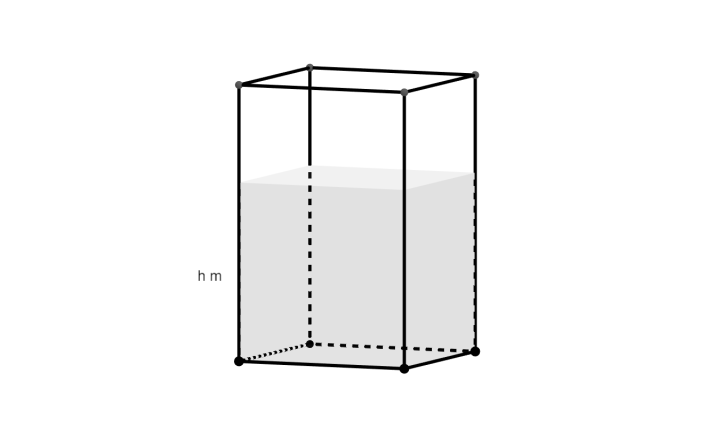
A water tank has vertical sides and a horizontal rectangular base, as shown in the diagram. The area of the base is $2\text{ }{{\text{m}}^{2}}$. At time $t=0$, the tank is empty and water begins to flow into it at a rate of $1\text{ }{{\text{m}}^{3}}$ per hour. At the same time, water begins to flow out from the base at a rate of $0.2\sqrt{h}\text{ }{{\text{m}}^{3}}$ per hour where $h\text{ m}$ is the depth of water in the tank at time $t$ hours. Form a differential equation satisfied by $h$ and $t$, and show that the time $T$ hours taken for the depth of water to reach $4\text{ m}$ is given by $T=\int\limits_{0}^{4}{\dfrac{10}{5-\sqrt{h}}dh}$.

Answer 1

Hint: We will calculate the volume of water in the tank when the water is at $h\text{ m}$ depth. The volume of water is changing with time. We will use the information of the rate at which water is flowing into the tank and the rate at which water is flowing out of the tank to formulate a differential equation that will represent the change in volume of water with respect to time.

Complete step by step answer:
The shape of the water tank is a cuboid. So, the volume of water in the tank can be calculated using the formula for the volume of a cuboid. The volume of a cuboid is given by $V=l\times b\times h$ where $l$ is the length of the tank, $b$ is the breadth of the tank and $h$ is the height. In this case, $h$ is the height upto which water is filled in the tank.
We know that the base of the tank has area $2\text{ }{{\text{m}}^{2}}$. That means, $l\times b=2$. So, the volume of water in the tank is given by, $V=l\times b\times h=2h\text{ }{{\text{m}}^{3}}$.
The volume of the water in the tank changes as follows:
(i) At time $t=0$, the tank is empty and water begins to flow into it at a rate of $1\text{ }{{\text{m}}^{3}}$ per hour.
(ii) At time $t=0$, water begins to flow out from the base at a rate of $0.2\sqrt{h}\text{ }{{\text{m}}^{3}}$ per hour.
The change in the volume of water with respect to time is given by $\dfrac{dV}{dt}$. Using the given information regarding the change of volume of water, we will form a differential equation in the following manner,
$\dfrac{dV}{dt}=1-0.2\sqrt{h}$
We know the volume of water in terms of $h$ at any time. It is $V=2h$. Substituting this value in the above equation, we get
$\begin{align}
  & \dfrac{d\left( 2h \right)}{dt}=1-0.2\sqrt{h} \\
 & \therefore 2\dfrac{dh}{dt}=1-0.2\sqrt{h} \\
 & \therefore \dfrac{dh}{dt}=0.5-0.1\sqrt{h} \\
\end{align}$
We have obtained a differential equation satisfied by $h$ and $t$.
Now, to calculate the time $T$ hours taken for the depth of water to reach $4\text{ m}$ we will use the differential equation we have formed.
We will separate the variables of the differential equation as follows,
$\dfrac{dh}{0.5-0.1\sqrt{h}}=dt$
Next, we will integrate both sides of the above equation in the following manner,
$\int{\dfrac{dh}{0.5-0.1\sqrt{h}}}=\int{dt}$
As the depth of the water changes from 0 to 4 with respect to time, we will set the limits of the integral on the left hand side as 0 and 4 for lower limit and upper limit respectively. On the right hand side, we will get the time $T$ hours taken for the depth of water to reach $4\text{ m}$. Therefore, we will write $T=\int{dt}$. Putting this information in the above equation, we get
 $\int\limits_{0}^{4}{\dfrac{dh}{0.5-0.1\sqrt{h}}}=T$
Now, we will rearrange the above equation to get the required answer in the following manner,
$\begin{align}
  & T=\int\limits_{0}^{4}{\dfrac{dh}{0.5-0.1\sqrt{h}}} \\
 & =\int\limits_{0}^{4}{\dfrac{dh}{\left( \dfrac{5}{10}-\dfrac{\sqrt{h}}{10} \right)}} \\
 & =\int\limits_{0}^{4}{\dfrac{10}{5-\sqrt{h}}dh}
\end{align}$
Hence, we get the equation $T=\int\limits_{0}^{4}{\dfrac{10}{5-\sqrt{h}}dh}$.

Note: While writing the differential equation, we used a positive sign for the rate of water flowing into the tank as the volume is increasing. Hence, we used the negative sign for the rate of water flowing out of the tank because the volume of water is decreasing.