Question

A water jet from a fountain reaches its maximum height of $4m$ at a distance $0.5m$ from the vertical passing through the point O of the water outlet. The height of the jet above the horizontal OX at a distance of $0.75m$ from the point O is
$(a). 5m$
$(b). 6m$
$(c). 3m$
$(d). 7m$

Answer 1

Hint:
We need to figure out what is given. Here we get the parabola and we can also have the value of height and distance once we mark the point in a diagram we can easily get the height of the jet when the distance is $0.75m$ by using roots of the parabola.

Complete step by step solution:
A water jet from a fountain reaches its maximum height of $4m$ at a distance $0.5m$ from the vertical passing through the point O of the water outlet. So the jet starts at the initial point $0$ which means $(0,0)$ and reaches the maximum height of $4m$ a distance $0.5m$ which means $(0.5,4)$ and the end point $(0,1)$ We need to find the height at a distance of $0.75m$ which means $(0.75,h)$.

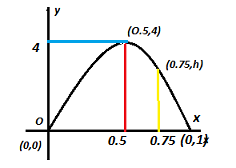
This represents the parabola, now we need to find the height of the jet above the horizontal OX at a distance of $0.75m$ from the point O
This is the parabola so the roots of the parabola are
$\Rightarrow y=a(x-r)(x-s)$
We take the point $(0,1)$ as $r=0,s=1$
Apply this to the roots of the parabola,
$\Rightarrow y=a(x-0)(x-1)$
$\Rightarrow y=ax(x-1)\to (1)$
Now we take the maximum height of $4m$at a distance of $0.5m$ so the $x$ coordinate is $0.5m$ and $y$coordinate is $4m$. Apply this to equation $(1)$
$\Rightarrow 4=a(0.5)(0.5-1)$
Multiply this we get,
$\Rightarrow 4=a(0.5)(-0.5)$
$\Rightarrow a=-\dfrac{4}{(0.5)(0.5)}$
Multiply and divide by $100$ to take the decimal out
$\Rightarrow a=-\dfrac{400}{25}$
$\Rightarrow a=-16$
Now apply this to equation $(1)$we get,
$\Rightarrow y=-16(x)(x-1)\to (2)$
Now using this we can the height of the jet above the horizontal OX at a distance of $0.75m$, thus the $x$ coordinate is $0.75m$ and $y$coordinate is $h$
Apply this to equation $(2)$
$\Rightarrow h=-16(0.75)(0.75-1)$
$\Rightarrow h=-16(0.75)(-0.25)$
Multiply this we get,
$\Rightarrow h=3m$

The height of the jet above the horizontal OX at a distance of $0.75m$ from the point O is $3m$.

Note:
One more example for parabola, when liquid is rotated the forces of gravity result in the liquid forming a parabola-like shape. Definition of parabola is, it’s a locus of such a point which has an equal distance from a fixed line and a fixed point. The value of eccentricity for parabola is one.